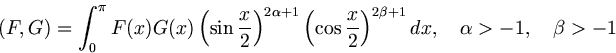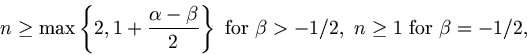Published in: Izv. Ross. Akad. Nauk, Ser. Mat., 68 (1998), no. 6,
pp. 27-52.;
English translation: Russian Acad. Sci. Math. Izv., 68 (1998), no. 6.
A B S T R A C T
B a b e n k o A. G.
Exact Jackson - Stechkin Inequality for
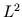 - Approximations on the Segment with Jacobi Weight
and on Projective Spaces
- Approximations on the Segment with Jacobi Weight
and on Projective Spaces
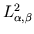 be a Hilbert space of real functions on
the segment
be a Hilbert space of real functions on
the segment ![$[0,\pi]$](img3.gif) with the inner product
with the inner product
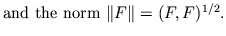 In the paper had been proved that
exact Jackson - Stechkin inequality
In the paper had been proved that
exact Jackson - Stechkin inequality
among the best approximation of the function 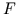 by cosine
polynomials of the order
by cosine
polynomials of the order 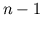 and its generalized modulus of
continuity of the (real) order
and its generalized modulus of
continuity of the (real) order 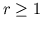 is valid
in the case
is valid
in the case
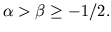 Here
Here
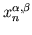 is the first positive zero of Jacobi cosine polynomial
is the first positive zero of Jacobi cosine polynomial
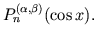
Analogouse results for mean squared approximations of functions
of many variables given on the projective spaces
are deduced from here.
Bibliogr. 49 titles.