Published in: Trudy Mat. Inst. im. V.A. Steklova 219 (1997), pp. 44-73;
English translation: Proc. of the Steclov Inst. of Math. 219 (1997), pp. 36-65.

A B S T R A C T

On Delsarte Scheme of Estimating Contact Numbers

V.V.Arestov and A.G.Babenko

In this work we study an extremal problem for functions continuous on an interval which are representable by series with respect to orthogonal polynomials with restrictions imposed on the values of the functions and the expansion coefficients, which is encountered in the investigations of Ph.Delsarte of the bounds of packings in certain metric spaces. Delsarte idea was developed and successfully used in the works of Ph.Delsarte, J.M.Goethalts and J.J.Seidel, G.A.Kabatyanskii and V.I.Levenstein, A.M.Odlyzko and N.J.A.Sloane, V.I.Levenstein, and V.M.Sidel'nikov, in particular, for investigation of contact number $\tau_m$ of the Euclidean space ${\Bbb R}^m$ which is equal to the maximal number of balls of unit radius with nonintersecting interiors which simultaneously touch the unit ball of the space. The exposition of these results and rich bibliography on this subjects can be found in the monograph of J.H.Conway and N.J.A.Sloane, Sphere packings, lattices and groups, Springer Verlag, New York, 1988. At present, the exact value of $\tau_m$ is known only for $m=2,3,8,24$, namely, $\tau_2=6,\ \tau_3=12, \tau_8=240$, $\tau_{24}=196\,560$. For arbitrary values of $m$ the lower and upper estimates of the constant $\tau_m$ are known; for instance, in the four-dimensional case we have $24\le\tau_4\le 25$.

Suppose that $\alpha=(m-3)/2$ and that $R_k=R_k^{\alpha,\alpha}$, $k=0,1,2,\dots,$ is a system of ultraspherical polynomials which are orthogonal on the interval $[-1,1]$ with respect to weight function $(1-t^2)^\alpha$ and which are normalized by the condition $R_k(1)=1, \ k=0,1,2,\ldots$ We denote by ${\cal F}_m(s)$ a set consisting of all continuous functions $f$ on $[-1,1]$ which are non-positive on $[-1,1/2]:$ $f(t)\le 0,$ $t\in [-1,1/2],$ and represented on $[-1,1]$ by series $f(t)=f_0R_0(t)+f_1R_1(t)+f_2R_2(t)+\ldots$ with non-negative coefficients $f_k\ge 0, \ k\ge 1,$ and $f_0>0.$ On this set of functions we consider the quantity

$$w_m=\inf\left\{\frac{f(1)}{f_0}: \ f\in{\cal F}_m\right\}.\eqno (*)$$

In the papers of Ph.Delsarte, J.M.Goethalts and J.J.Seidel, G.A.Kabatyanskii and V.I.Levenstein, A.M.Odlyzko and N.J.A.Sloane it was proved that arbitrary function $f\in{\cal F}_m$ gives the estimation $\tau_m\le f(1)/f_0,$ therefore the inequality $\tau_m\le w_m$ holds. In such a way at the expense of a choice of concrete functions $f\in{\cal F}_m$, V.I.Levenstein, A.M.Odlyzko and N.J.A.Sloane have received good estimations from above of contact numbers $\tau_m,$ in particular, have calculated $\tau_8, \tau_{24}$.

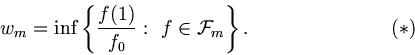
The following is done in this article. A dual problem is written out and the corresponding duality theorem is given for a problem which is somewhat more general than $(*).$ The exact solution of problem $(*)$ is given for $m=4$. It has turned out that the solution is a polynomial which is close to the polynomial written out earlier in the work of A.M.Odlyzko and N.J.A.Sloane, New bounds on the number of unit spheres that can touch a unit sphere in $n$ dimensions, Journal of Combinatorial Theory, Series A, 26 (2) (1979), 210-214. Our result signifies that inequality $\tau_4\le w_4$ cannot give, for the number $\tau_4$, an upper estimate that would be better than the upper estimate $\tau_4\le 25$ obtained by A.M.Odlyzko and N.J.A.Sloane.

Bibliogr. 21 ref.