Description of main results (1983-2001).

1983-1984. An arbitrary space $P_n$ arising from a $2\pi$-periodic Chebyshev system $\{1,$ $\varphi_1,$ $\varphi_2,$ $\ldots,$ $\varphi_{2n}\}$ and invariant with respect to a translation of $2\pi/(n+1)$ is considered. Let

$$m(P_n):=\inf\{\,{\rm mes}(\,x\in[0,2\pi]:\;f(x)\ge0\,):\; f\in{P^0_n}\,\},$$

where $P^0_n$ is the set of polynomials $f\in{P_n}$ with zero mean. It is proved that $m(P_n)=2\pi/(n+1).$

The important example $P_n$ is the space of trigonometric polynomials of degree $n.$ The problem appropriate to trigonometric case was put by L.V.Taikov in the beginning 60th years of XX century.

1985. Let $X$ be an infinite-dimesional linear normed space and $B:=\{x\in X:\; \Vert x\Vert\leq1\}$ its unit ball. We prove that for any fixed number $\delta\in(0,1)$ there exists a continuous mapping $T$ of the ball $B$ into itself such that $\Vert x-Tx\Vert\geq\delta$ for all $x\in{B}.$

1986-1988. Let $E_{n-1}(f)$ be the best trigonometric $L^2$-approximation of order $n-1$ of a $2\pi$-periodic function $f\in L^2,$ and let $\omega(f,\delta)$ be the modulus of continuity of $f$ in $L^2.$ The smallest constant $K=K_n(\tau)$ in the Jackson inequality

$$E_{n-1}(f)\leq K\omega\left(f,\frac{\tau}{n}\right),\quad f\in L^2,$$

is found for

$$\tau=\frac{\pi}{m},\quad m\in{\bf N},\quad m\geq1+\frac{3n}{2},\quad n\geq1,$$

and for

$$\tau=\frac{\pi}{m},\quad m\in{\bf N},\quad m\geq\frac{3n}{4},\quad n\geq10.$$

In particularly, it is proved that

$$K_n(\tau)= \sqrt{\frac{1}{2}+\frac{\cos(\tau/2)-1/2}{\tau\sin(\ta... ...d \tau=\frac{\pi}{m},\quad m\in{\bf N},\quad m\geq1+\frac{3n}{2},\quad n\geq1.$$

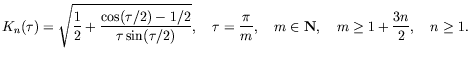
The analogous results are obtained for mean square approximations of periodic functions by trigonometric polynomials on a uniform net.

1996-1998. It is proved exact Jackson-Stechkin inequality

$$E_{n-1}(f) \leq \omega_r (f,2 \tau _{n,\lambda}), \quad f\in L^2({\bf S}^{m-1}),$$

for any fixed $n\geq1,\;m\geq5,\;r\geq1.$ Here $E_{n-1}(f)$ is the best $L^2$-approximation of a function $f\in L^2({\bf S}^{m-1})$ by spherical polynomials of degree at most $n-1,$ $\omega _r(f,\tau)$ is the $r$th modulus of continuity of $f$ based on translation

$$s_t f(x):=\frac{1}{\vert{\bf S}^{m-2}\vert}\int_{{\bf S}^{m-2}} f(x\cos t+\xi\sin t)d\xi ,$$

$$t\in{\bf R},\quad x\in{\bf S}^{m-1},\quad {\bf S}^{m-2}={\bf S}^{m-2}_x= \{\xi\in{\bf S}^{m-1}:\; x\cdot\xi=0\},$$

$\vert{\bf S}^{m-2}\vert$ is the measure of the unit Euclidean sphere ${\bf S}^{m-2},$ $\lambda=(m-2)/2,\ \ \tau_{n,\lambda}\$ is the first positive zero of the Gegenbauer's cosine polynomial $C^{\lambda}_n (\cos t)$.

Let $L^2_{\alpha,\beta}$ be a space of real quadratically integrable functions on the segment $[0,\pi]$ with the Jacobi weight function $(\sin(x/2))^{2\alpha +1}(\cos(x/2))^{2\beta +1},$ $\;\alpha>\beta\ge-1/2\;$ or $\;\alpha=\beta>-1/2.$ The following exact Jackson-Stechkin inequality has been proved

$$E_{n-1} (f) \le \omega_r (f,2x_{n}^{\alpha,\beta}), \quad f\in L^2_{\alpha,\beta},\quad r\ge 1,$$

$n\geq1\;$ for $\;\alpha>\beta=-\displaystyle\frac{1}{2}\;$ or $\;\alpha=\beta>-\displaystyle\frac{1}{2}\;$ and $\;n\ge\max\left\{2,1+\displaystyle{\frac{\alpha-\beta}{2}}\right\}\;$ for $\alpha>\beta>-\displaystyle\frac{1}{2}.$ Here $E_{n-1}(f)$ is the best approximation of a function $f$ by a cosine polynomial of degree at most $n-1$ in $L^2_{\alpha,\beta}$-metric and $\omega _r(f,\tau)$ is the $r$th modulus of continuity based on the operator of generalized translation in $L^2_{\alpha,\beta};$ $x_{n}^{\alpha,\beta}$ is the first positive zero of Jacobi cosine polynomial $P_{n}^{(\alpha,\beta)}(\cos x).$

The analogous exact inequalities are obtained for mean square approximations of functions of several variables given on the Euclidean and projective spaces. These results expand the known sharp results of N.I.Chernykh, V.A.Yudin, V.V.Arestov and V.Yu.Popov.

2000-2001. It is considered the Jackson-Stechkin inequality between the best mean square approximation of an arbitrary $2\pi$-periodic function $f\in L^2$ by finite-dimensional subspace $X\subset L^2$ and modulus of continuity (smoothness) of $f$ generated by a finite difference operator with coefficients (weights) depending continuously on the step of the operator. The universal (independent of $X$) lower bound for the exact constant in the described inequality is obtained. This bound is sharp in a number of cases.

The exact results in this direction for the case of the classical modulus of continuity of the first order in spaces $C$ and $L^p$ were established by N.P.Korneichuk (1962-1984), N.I.Chernykh (1967-1992), V.I.Berdyshev (1967-1985) and other mathematicians.

The mentioned above finite difference operator and corresponding modulus of continuity are connected with divided and finite differences, generalized moduli of continuity (smoothness) which were investigated and used by T.Popoviciu (1959), J.Boman and H.S.Shapiro (1971), G.Mühlbach (1973), A.Sharma and J.Tzimbalario (1977), Ch.A.Micchelli (1979), V.T.Shevaldin (1981), R.B.Barrar and H.L.Loeb (1984), Z.Wronicz (1984), Gh.Toader and S.Toader (1985) and other mathematicians.

Below we describe the results received jointly with V.V.Arestov.

1997-2000. Let ${\cal R}=\{R_k\}_{k=1}^{\infty}$ be an uniformly bounded sequence of continues real functions on compactum $Q\subset(-\infty,\infty)$, and $G$ denote set of all non-negative summable sequences $x=\{x_k\}_{k=1}^{\infty}$ such that $1+x_1{R_1(t)}+x_2{R_2(t)}+\ldots\le 0, \ t\in Q.$ If $G\ne\emptyset$, let us consider the minimization problem for the functional $U(x)=x_1+x_2+\ldots$ on $G$. Delsarte's method on upper bounds for packings in some metric spaces lead to the problem for special functional system ${\cal R}$. We wrote dual problem for mentioned problem and proved corresponding duality theorem including existence of solutions of the both problems. Additional properties of the solutions was indicated in the case when $Q\subset[-1,1)$ and ${\cal R}$ is the system ${\cal R}^{(\alpha,\beta)}=\{R_k^{(\alpha,\beta)}\}^\infty_{k=1}, \ R_k^{(\alpha,\beta)}(1)=1$ of Jacobi polynomials where $\alpha\ge\beta\ge-1/2$. For ${\cal R}={\cal R}^{(1/2,1/2)}, \ Q=[-1,1/2]$, it was found exact solutions of these problems which are connected with the kissing number problem in ${\bf R}^4$.

Possibilities of the Delsarte scheme for upper bounds of minimal distances in the sets which consist of 24 and 25 points on the unit sphere of the Euclidean space ${\bf {R}}^4$ were shown. As consequence, it is obtained that among arbitrary $25$ $(24)$ points located on unit sphere in ${\bf {R}}^4$ there exist two points with the angular distance between them strictly less than $60.5^{\circ}$ $(61.41^{\circ})$.

2001-2002. Denote by ${\cal K}_{r}(\delta,\sigma),\;r>0,\;\delta>0,\;\sigma>0,$ the least constant in the Jackson inequality

$$E_{\sigma}(f)\le {\cal K}_r(\delta,\sigma)\ \omega_r(\delta,f), \quad f \in L^2({\bf {R}}),$$

between the best approximation $E_{\sigma}(f)=\inf\{\,\Vert f-g\Vert _{2}:\ g\in W(\sigma)\,\}$ of a function $f\in L^2({\bf {R}})$ by the space $W(\sigma)$ of entire functions of exponential type $\sigma$, on the left hand, and its $r$th modulus of continuity $\omega_r(\delta,f)$ on the other hand. We proved that ${\cal K}_{r}(\delta,\sigma)$ is continuous with respect to $\delta.$