Published in Research Communications of the conference held in the memory of Paul Erdos Budapest, Hungary, July 4-11, 1999, ed. A. Sali, M. Simonovits and V.T. Ss, J
nos Bolyai Math. Soc., Budapest, 1999, pp. 10-14.
Introduction. Let ![]() denote the unit sphere in
real Euclidean
denote the unit sphere in
real Euclidean ![]() -dimensional space
-dimensional space
![]()
![]() where
where
![]() is the inner product of vectors
(points)
is the inner product of vectors
(points)
![]()
![]() . For
. For ![]() a set
a set
![]() containing at
least two points is called a spherical
containing at
least two points is called a spherical ![]() -code, if for any
two points
-code, if for any
two points
![]() their inner product
their inner product ![]() satisfies to the condition
satisfies to the condition ![]() This condition means that an
angular distance (angle) between any pair of distinct points in
This condition means that an
angular distance (angle) between any pair of distinct points in ![]() is greater than or equal to
is greater than or equal to ![]() :
:
The basic problem for spherical codes can be formulated as follows:
for given ![]() and
and ![]() find a spherical
find a spherical ![]() -code
-code
![]() of largest possible size
of largest possible size ![]() . We denote
this maximal size by
. We denote
this maximal size by ![]() This problem can be consider in the
inverse form: for given
This problem can be consider in the
inverse form: for given ![]() and
and ![]() find a spherical
code
find a spherical
code
![]() with largest possible minimal
angle
with largest possible minimal
angle
![]() , which we denote by
, which we denote by ![]() i.e.
i.e.
In the articles [9], [10], Levenstein
obtained universal upper bound for the quantity ![]() Levenstein's result can be reformulated for estimating
Levenstein's result can be reformulated for estimating
![]() (cf. [2]); in particular,
(cf. [2]); in particular,
The arrangement of ![]() points on
points on ![]() with the minimal
angle
with the minimal
angle
![]() was constructed by Hardin, Sloane and
Smith [7]. Thus, the following estimations
are fulfilled:
was constructed by Hardin, Sloane and
Smith [7]. Thus, the following estimations
are fulfilled:
Delsarte method. The method which arose in investigations of
Delsarte [4] on upper bounds for packings in some
metric spaces is often used for estimating from above the
quantities
![]() This method was developed and
successful applied in the works [5],
[8], [11],
[9], [10],
[2] and in of many other articles; the
rich bibliography on the subject is contained in monograph
[3].
This method was developed and
successful applied in the works [5],
[8], [11],
[9], [10],
[2] and in of many other articles; the
rich bibliography on the subject is contained in monograph
[3].
Let
![]()
![]() be the
system of ultraspherical (Gegenbauer) polynomials which are
orthogonal on interval
be the
system of ultraspherical (Gegenbauer) polynomials which are
orthogonal on interval ![]() with respect to weight function
with respect to weight function
![]()
![]() and normed by
condition
and normed by
condition ![]() The mentioned approach is founded on a
positive-definite property of these polynomials (if we will
consider them as kernels
The mentioned approach is founded on a
positive-definite property of these polynomials (if we will
consider them as kernels ![]() on on the Cartesian product
on on the Cartesian product
![]() ).
).
For
![]() denote by
denote by ![]() a set
consisting of all continuous functions
a set
consisting of all continuous functions ![]() on
on ![]() which are
non-positive on
which are
non-positive on
![]() and
represented on
and
represented on ![]() by series
by series
![]() with non-negative
coefficients
with non-negative
coefficients
![]() and
and ![]() The fact that
The fact that
![]() is non-empty for all
is non-empty for all
![]() was
proved in [8]. Let us put
was
proved in [8]. Let us put
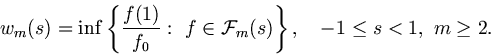
The following statement is contained in [5], [8].
Theorem A. Let
![]() Then
Then
![]()
Formulation of results. Further we consider four-dimensional
case (![]() ) only. In this case index
) only. In this case index ![]() is equal to
is equal to ![]() and the polynomials
and the polynomials
![]() are Chebyshev polynomials
of the second kind:
are Chebyshev polynomials
of the second kind:
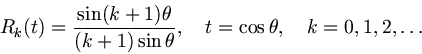
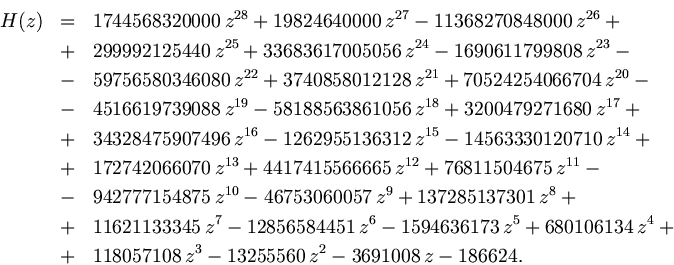
Theorem 1. In ![]() the equation
the equation
![]() has the unique solution:
has the unique solution: ![]() where
where
![]() is thirteenth
is thirteenth ![]() on the increase
on the increase![]() real root of polynomial
real root of polynomial ![]()
Consider the polynomial
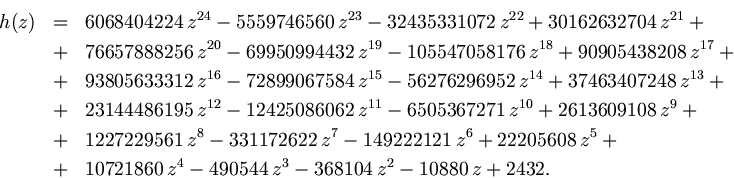
Theorem 2. In ![]() the equation
the equation
![]() has the unique solution:
has the unique solution: ![]() where
where
![]() is twelfth
is twelfth ![]() on the increase
on the increase![]() real
root of polynomial
real
root of polynomial ![]()
Corollary. Among arbitrary ![]()
![]() resp.
resp.
![]() points located on
points located on
![]() there exist
two points with the angle between them strictly less than
there exist
two points with the angle between them strictly less than
![]()
![]() resp.
resp.
![]() . Thus,
. Thus,
Let us remind also (see (1), (2)) that the answer to the question:
"whether is the least angular distance between pairs of points of
arbitrary configuration of ![]() points on
points on ![]() strictly less
than
strictly less
than ![]() degrees?" should give a solution of the kissing number
problem in
degrees?" should give a solution of the kissing number
problem in ![]()
The theorem 1 implies that in order to find the number ![]() it
is necessary to use other methods. We hope that application of
results and ideas of Paul Erdös, his coauthors and pupils, in
particular, concerning properties of distribution of distances of
given number points on sphere [6], will
help to decide problems of such kind.
it
is necessary to use other methods. We hope that application of
results and ideas of Paul Erdös, his coauthors and pupils, in
particular, concerning properties of distribution of distances of
given number points on sphere [6], will
help to decide problems of such kind.