Иванов А.Г.
Екатеринбург, ИММ УрО РАН, iagsoft@imm.uran.ru
КЛАССИЧЕСКИЕ МОДЕЛЬНЫЕ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
В Уральском госуниверситете при преподавании вариационного исчисления большое внимание уделяется классическим модельным задачам вариационного исчисления. Задачи рассматриваются с разных точек зрения: решения получаются как аналитически, так и численно. Применяется учебно-демонстрационное программное обеспечение, разработанное при участии самих студентов.
Доклад посвящен следующим трем задачам.
Аэродинамическая задача Ньютона. Состоит в отыскании образующей
y = y(x) (граничные условия y(0) = 0 и y(1) = 1 ) тела вращения с наименьшим сопротивлением в потоке разреженного идеального газа. Разреженный газ представляется в виде бесконечно малых частиц, не сталкивающихся друг с другом и зеркально отражающихся от поверхности тела при столкновении с ним.Прежде всего задача решается, следуя [1], в предположении малости величины
y'2 . Соответствующее решение уравнения Эйлера имеет вид y = x3/4 (коэфф. сопротивления Cx = 0.22 ). После этого демонстрируется численный поиск решения в классе функций y = xp (минимальное значение Cx = 0.20 при y = x0.46).Аналитическое решение задачи с граничным условием
y(0) = 0 заходит в тупик. В рамках численного подхода демонстрируется программа поиска решения методом Эйлера (аппроксимация кусочно-линейной функцией). При этом задача сводится к отысканию минимума функции многих переменных. На основе полученного численного решения происходит переформулировка постановки задачи, после чего задача решается аналитически. Оптимальное решение (Cx = 0.19 ) имеет угловую точку [2].
Задача о наименьшей поверхности вращения. Необходимо отыскать образующую поверхности вращения, которая минимизировала бы площадь этой поверхности. Известно, что искомая образующая
- цепная линия. В зависимости от конкретных граничных условий могут существовать два решения уравнения Эйлера, одно или ни одного. При традиционном изложении не уделяется достаточного внимания случаю отсутствия классического решения. При численном решении методом Эйлера легко обнаруживается разрывное решение: два диска, образующей для которых служит ломаная, состоящая из двух вертикальных отрезков и одного горизонтального, лежащего на оси вращения. Показывается, что даже при существовании аналитического решения глобальный минимум может достигаться на дисках. Приводятся области граничных условий, для которых глобальный минимум достигается на различных типах решений.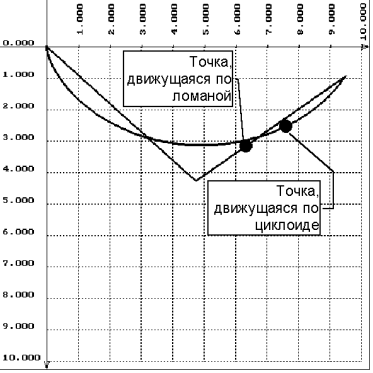
Задача о брахистохроне. В задаче необходимо найти линию наискорейшего спуска между двумя точками в вертикальной плоскости. Этой линией является дуга циклоиды. Проблема нахождения конкретной циклоиды для конкретных граничных условий обычно остается за рамками изложения. Создана программа, которая для любых допустимых граничных условий находит и графически изображает оптимальное решение в виде циклоиды и оптимальное решение в классе двухзвенных ломаных.
Рассматривается задача о брахистохроне в центральном поле тяготения (вариант интерпретации - движение заряженной частицы в поле неподвижной частицы противоположного заряда). Демонстрируется решение, полученное численно.
1. М.А.Краснов, Г.И.Макаренко, А.И.Киселев. Вариационное исчисление. М., "Наука", 1973.
2. И.Ньютонъ. Математическiя Начала Натуральной Философiи. П., 1916.