В 1687 году вышли "Математические начала натуральной философии" Ньютона. В "Отделе VII": "О движении жидкостей и сопротивлении брошенных тел" есть интересный абзац:
Когда же фигура DNFG будет кривою такого рода, что если из любой ее точки N опустить на ось перпендикуляр NM и из заданной точки G провести прямую GR параллельную касательной к кривой в точке N и пересекающую ось в точке R, то имеет место пропорция:Цитируется по [1], стр.383.
MN : GR = GR3 : 4BR . GB2 тогда тело, образующееся при обращении этой кривой около оси AB при движении в вышеупомянутой редкой среде в направлении от A к B будет испытывать меньшее сопротивление, нежели всякое иное тело вращения, описанное на той же длине и той же наибольшей ширине.
Как Ньютон пришел к такому решению, до сих пор остается непонятным. Некоторые авторы, в частности [2], считают, что в этом вопросе Ньютон был не прав. Здесь, пользуясь методами классического вариационного исчисления, применяя численные методы, детально проанализируем эту задачу.
Рассматриваемая Ньютоном среда состоит "из равных частиц свободно расположенных на равных друг от друга расстояниях". Причем, так как среда "редкая", то вероятность столкновения частиц между собой принимается равной нулю. Среда, кроме того, считается абсолютно упругой, то есть столкновение частиц среды с телом происходит по правилу: угол падения равен углу отражения; модуль скорости во время удара не изменяется (нет потерь энергии).
Ньютон рассматривает тела вращения симметричные относительно плоскости,
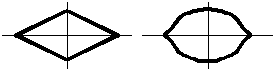 |
| Рис. 1 |
 |
| Рис. 2: Тела с одинаковой силой сопротивления |
Найти образующую y=y(x), y(0)=0, y(x1)=y1, x1>0, которая бы при вращении в пространстве xyz вокруг оси Ox, дала тело вращения с наименьшим сопротивлением при движении в отрицательном направлении оси Ox в рассматриваемой среде.
Далее, для определенности, возьмем x1=1, y1=1
|
| |
|
Кроме вышеупомянутых должны быть рассмотрены следующие естественные ограничения: a) y([0,1]) >= 0 б) форма образующей не допускающая повторных соударений частиц среды с телом. Другими словами, любая частица среды не должна ударяться о тело более одного раза. Если это условие не выполняется, то вывод функционала сильно усложнится. Достаточным признаком выполнения этого условия является выполнение y''(x) <= 0. |
Пока опустим условия, упомянутые в примечании 1, после получения результата просто проверим их выполнение.
Задания по теме:
![]() tasks.pdf (95K)
tasks.pdf (95K)
|
Вариационное исчисление | Домашняя страница | Электронные публикации | Печатные работы |
 iagsoft@imm.uran.ru
iagsoft@imm.uran.ru