(Екатеринбург,
Ключевые слова: дифференциальные уравнения, параллельные вычисления, восстановление параметров, информационные множества, асимметрический синтез, константа скорости реакции, динамическое кинетическое расщепление.
Асимметрические синтезы на основе процессов динамического кинетического расщепления представляют большой интерес, поскольку позволяют получить продукты, обогащенные одним стереоизомером из рацемического субстрата или смеси диастереомеров. Важные данные о механизме таких реакций и факторах, определяющих стереоселективность, можно извлечь из результатов изучения кинетики их протекания. Однако сложность расчетов (связанная с многокомпонентностью реакционных смесей, взаимным влиянием реактантов на скорости химических превращений и с погрешностью измерений) требует поиска новых подходов к математическому определению динамических параметров таких систем.
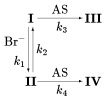 |
| Рис. 1 |
К реакциям указанного типа относится взаимодействие диалкиловых эфиров трео- и эритро-N-фталил-4-галогенглутаминовых кислот (I, II) с производными анилина (AS). Было установлено [1], что реакция протекает диастереоселективно, с образованием избытка трео-изомера (IV) продукта, по сравнению с эритро- (III). Исследования процесса показали, что нуклеофильное замещение галогена в диастереомерах субстрата, I и II, сопровождается их взаимным превращением, катализируемым выделяющимся галогенид-ионом. Поэтому процесс может быть представлен схемой, показанной на рис. 1, и описан системой дифференциальных уравнений
|
|
(1) |
Величины (A0 + B0) и E0 известны точно. Во время реакции в определенные моменты времени ti производятся замеры величин A(ti), B(ti), C(ti), D(ti). Точность величин описывается относительной (r) и абсолютной (q) погрешностями. Таким образом, подразумевается, что истинная величина Z(ti) (где Z заменяет одну из букв A, B, C, D) попадает в ``ворота замера'':
Первая задача состояла в определении хотя бы одной четверки значений констант k1, k2, k3, k4, при которых система (1)-(3) удовлетворяла бы имеющимся замерам. Для решения этой задачи была использована параллельная программа поиска минимума скалярной функции многих переменных [2].
В качестве целевой функции брались функции, аргументом которых был вектор значений k1, k2, k3, k4, а значением -- показатель, говорящий о том, выходит ли ``траектория'' химической реакции при рассматриваемых константах за установленные допуски. Было сконструировано три функции, обладающих данным свойством: при попадании в допуски значение функции отрицательно, при выпадении из хотя бы одного допуска -- положительно. В частности, одна из функций характеризует максимальное расстояние от границ допусков:
Для сравнения минимизировалась также функция, являющаяся суммой квадратов отклонений (метод наименьших квадратов):
В результате вычислительного эксперимента было установлено, что первоначальные параметры точности r и q были занижены -- не удалось найти четверки констант, удовлетворяющих всем замерам. После увеличения значений r и q удалось получить непротиворечивый набор k1, k2, k3, k4. Интересный факт состоит в том, что наилучший с точки зрения минимума суммы квадратов (4) набор в ряде случаев выходит за рамки допуска для нескольких замеров.
Задача решалась на машине МВС-100. Наилучшим оказалось количество процессоров равное 16, при большем числе процессоров скорость вычислений падала.
Вторая задача состояла в определении пределов изменения констант k1, k2, k3, k4, а также пределов изменения отношения s = k4/k3. Т.е. необходимо было построение четырехмерного (в пространстве k1, k2, k3, k4) информационного множества -- множества четверок констант, порождающих совместное со всеми замерами протекание реакции.
Для этого было организовано численное моделирование протекания реакции (1)-(3) при задании констант на прямоугольной четырехмерной сетке. В случае попадания смоделированных значений концентраций в ``ворота'' всех замеров считается, что узел сетки принадлежит информационному множеству, в противном случае -- нет. Для изображения четырехмерного множества были выбраны проекции на плоскости k1, k2 и k3, k4.
Создана параллельная программа на языке ``Си'' для МВС-100/1000 (операционная система ROUTER [3]). Один процессор назначается процессором вывода, все остальные -- рабочими. Рабочие рассчитывают сетки по k3, k4 при фиксированных значениях k1, k2. Если хотя бы один узел сетки оказывается совместным, то сетка по k3, k4 с помеченными совместными узлами передается на процессор вывода. Таким образом, передача ведется только в случае непустой сетки, что несколько уменьшает общий трафик процессорной сети. Процессор вывода принимает сетки от рабочих, формирует проекции информационного множества на плоскости k1, k2 и k3, k4, записывает рисунки проекций в графические метафайлы. Максимальные размеры сетки в существующем варианте программы 126 × 126 × 126 × 126 узлов. Вычисления велись на МВС-100 на сети из 125 процессоров.
Результатом работы программы являются проекции (на плоскости k1, k2 и k3, k4) информационного множества для системы (1)-(3).
Использование описанного подхода позволяет обоснованно рассчитать константы скоростей элементарных реакций процесса динамического кинетического расщепления и допуски на них с учетом реальных погрешностей измерений.
| [1] | Краснов В.П., Королева М.А. Нуклеофильное замещение галогена в 4-галогенпроизводных глутаминовой кислоты. Сообщение 1. Влияние растворителя // Изв. АН, Сер. хим., 1995, N4. С. 652-655. |
| [2] | Иванов А.Г. Параллельный алгоритм прямого поиска минимума функции многих переменных2 // Алгоритмы и программные средства параллельных вычислений: [Сб. науч. тр. Вып. 2.]. Екатеринбург, 1998. С. 110-122. |
| [3] | Лацис А.O. Операционная среда ROUTER для транспьютерных систем. Документация по МВС-100. |
| е-mail: | iagsoft@imm.uran.ru (Иванов А.Г.), | |
| ca@ios.uran.ru (Краснов В.П.), | ||
| kumkov@imm.uran.ru (Кумков С.И.) |

|
Главное меню | Публикации | Электронные публикации | Обо мне | |