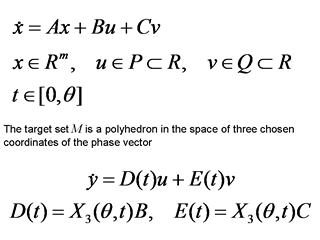Russian version

Ivanov A.G., Ushakov A.V.

Adaptive Control in Three-Dimensional Linear Systems with Dynamical Disturbance of Unknown Level

Game Theory and Management
Second International Conference on Game Theory and Management

Download full text of the report (PDF format, 3374 KB)

Slide 1

The first part of presentation is devoted to constructing the maximal stable bridges in the three-dimensional (by the target set) linear differential game. In the second part, the procedure elaborated is applied to building an adaptive control in problems where there is no a priori geometric constraint for the second player's control.

Slide 2

Maximal stable bridges construction

Differential game in the original space and the equivalent game

Slide 3

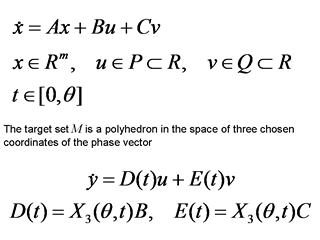
In the original game, the phase vector can have any dimension m ≥ 3, but the convex target set depends only on three selected components of the phase vector. By the standard change of variables, we pass to the equivalent differential game of the third order without phase variables in the right-hand side of its dynamics. We assume that the constraints P, Q onto the controls of the first and second players are segments.

Approximating game

Slide 4

For constructing the maximal stable bridge in the approximating game, we divide the time axis into a grid {t_i} with the step Δ to the left from the termination instant θ, and, under this, t₀=θ. On each time step, we "freeze" the dynamics of the equivalent system. As a result, we obtain a collection of time sections (t-sections) W_i=W(t_i) ⊂ R³ of the approximating maximal stable bridge W.

The construction of the time sections is implemented in a backward procedure: in the first step, on the basis of the target convex polyhedron, a convex polyhedron W₁ is built; in the second step, on the basis of the polyhedron W₁, a convex polyhedron W₂ is built, and so on.

The construction of each next section W_i+1 of the bridge includes operations with convex polyhedrons, namely, constructing the algebraic sum (Minkowski sum) F_i of the polyhedron W_i and the segment −Δ·P_i (this takes into account the action of the first player) and constructing the geometric difference (Minkowski difference) of the polyhedron F_i and the segment Δ·Q_i (this takes into account the action of the second player). The latter procedure is equivalent to building the convex hull of the difference ρ(·, F_i) − ρ(·, Δ·Q_i) of the support functions of the sets F_i and Δ·Q_i.

For a continuous, positive homogeneous, and piecewise linear function γ : l → γ(l) with convex cones of linearity, we use the following representation: on the unit sphere S, we introduce a grid (graph) G(γ), which is defined by the intersection of the sphere with the linearity cones of the function γ. At each node of G(γ), the value of the function γ is written.

When constructing the support function ρ (·, W_i+1) of the polyhedron W_i+1, we require that all linearity cones of the function ρ(·, W_i) are three-edged and, respectively, the cells of the grid G(ρ(·, W_i)) are triangular. For this, it is necessary to triangulate the initial grid, and further, when constructing new grids, to apply (if necessary) additional triangulation of the grid.

Taking into account action of the first player

Slide 5

The grid G(ρ(·, F_i)) is the result of overlapping the grids G(ρ(·, W_i)) and G(ρ(·, P_i)). Since P_i is a segment in R³, the graph G(ρ(·, P_i)) is a circumference on the sphere S, i.e., the intersection of the sphere and the plane passing through the origin and orthogonal to P_i. When overlapping the grids, new nodes appear. So, when constructing the grid G(ρ(·, F_i)), we establish additional links to provide the linearity cones of the function ρ(·, F_i) to be three-faced.

Taking into account action of the second player

Slide 6

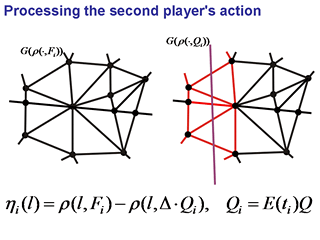
We recompute values of the support function ρ(·, F_i) at the nodes of the grid G(ρ(·, F_i)) with taking into account action of the second player, and we obtain a function η_i(·).

To pass to the support function of the polyhedron W_i+1, it is necessary to exclude the nodes of the graph G(ρ(·, F_i)), where the convexity of the function η_i(·) is violated.

To implement the convexification, a special iterative procedure was elaborated. Collect "suspicious" links into a list. Initially, we put there that links of the grid G(ρ(·, F_i)), which intersect with the graph G(ρ(·, Q_i)), and links in incident to them. Further, a correction of these links is implemented; this procedure corrects the violations of the local convexity. Under this, the list of suspicious links can be added with other links. Vice versa, the links, where the local convexity takes place, are excluded from the list. This process is ceased when the list of suspicious links becomes empty.

Groundwork

Slide 7

To elaborate the algorithm for constructing the maximal stable bridge, we used ideas from the cited papers.

Algorithm of constructing the maximal stable bridge

Slide 8

The scheme of the algorithm for constructing the stable bridge is presented. It is based on the stepwise procedure for building the time sections. The iterative procedure of convexification is the most expensive in computations of each next section.

Model examples

Slide 9

In the case k = 0, the dynamics shown in the slide describes the motion of an inertial point along the direct line. In the case k = 1, a conflict-controlled oscillator is described. The first player governs the control u, the second player governs the control v.

Finding the value function in a two-dimensional game (by means of a three-dimensional bridge)

Slide 10

In a two-dimensional game with fixed termination instant, the terminal payoff function γ is taken as γ(x) = max{|x₁|, |x₂|}. We are interested to get the value function.

To construct the epigraph of the value function, consider a game of the third order with the target set M as the cut-off (at a level c^*) of the epigraph of the payoff function for the two-dimensional game. Then, a t-section of the bridge of the three-dimensional game will be the cut-off (at the level c^*) of the epigraph of the value function for the two-dimensional game at the same instant t.

Target set

Slides 11, 12

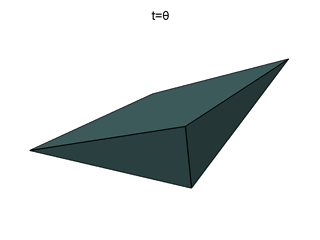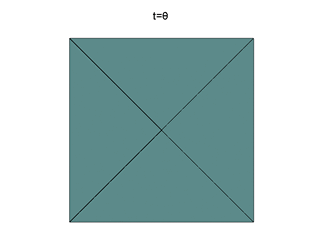
Here, the target set of the three-dimensional game is presented: side view and bottom view.

Time sections of the bridge for several instants

Slides 13–22

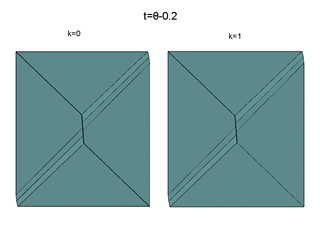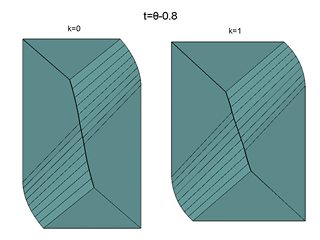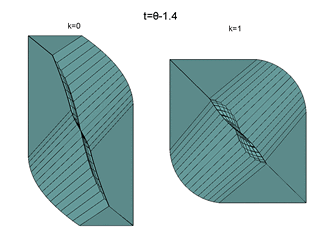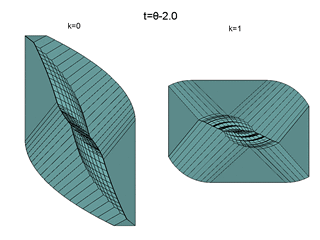
Here, the t-section of the bridges for different instants are presented for the considered three-dimensional games: at the left, for the inertial point; at the right, for the pendulum. These are views from "below", i.e., from the side of negative values of the c-axis.

Slide 23

Adaptive control

Adaptive control

Slide 24

We consider a problem of constructing an adaptive control in linear systems with unknown level of the dynamic disturbance. The aim of useful control is to guide n selected components of the phase vector to a convex bounded target set at the fixed terminal instant θ. The useful control obeys a geometric constraint. The dynamic disturbance (the second player's control) is assumed to be bounded, but the level of its constraint is unknown a priori.

Principle of the adaptive control

Slide 25

Here, the requirements to the adaptive control are presented.

Family of stable bridges for constructing adaptive control

Slide 26

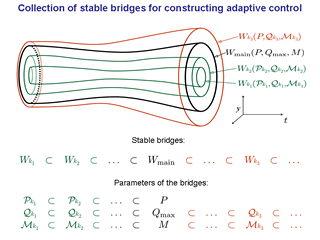
An ordered family of the stable bridges is considered. Each bridge is defined by a triple: the constraint for the first player's control, the constraint for the second player's control, and the target set.

The main bridge W_main corresponds to the triple P, Q_max, and M. Here, the sets P and M are given by the problem formulation, and the set Q_max is chosen by us and can be treated as a constraint for the disturbance, which is assumed to be "reasonable" in the problem under consideration. We assume that each of the sets P, Q_max, and M contains the origin of its space.

For the case n = 2, the algorithms for constructing the adaptive control were worked out earlier. The picture of the embedded system of bridges is presented just for such a case.

In this work, we consider the case of a three-dimensional target set. Therefore, the t-sections of bridges are also three-dimensional. For constructing the bridges, we use the algorithm described in the first part of the presentation.

Simulation of the adaptive control

Slides 27–43

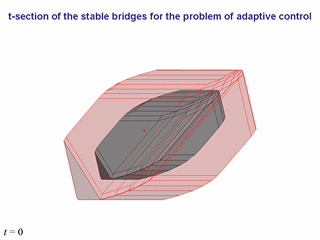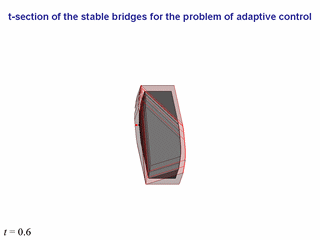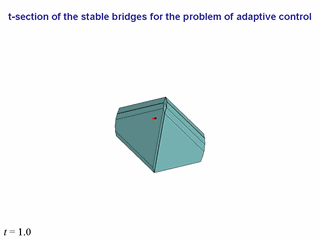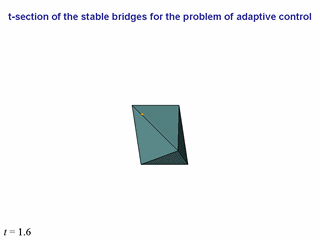
Now, let us present the simulation results for some dynamic system (we do not write it). To construct the adaptive control, we use the principle of extremal aiming well-known in the theory of differential games. The adaptive control is used for the first player; a random disturbance plays the role of the second player's control.

The following sequence of slides shows the behavior of the phase state of the system with respect to the t-sections of the main bridge.

In the initial interval of time, the phase point is out of the main bridge (it is the red colored point). Therefore, for constructing the adaptive control, t-sections of outer bridges are used. The pink color shows the section, which is used for the extremal aiming in the procedure of the adaptive control generating. At some instant, the phase point comes inside the main bridge (when inside, the point is colored in orange). In such situations, only the t-sections of the main bridge is shown, though the control is implemented by aiming to the t-section of some smaller bridge. The t-section of that bridge is computed very simply, namely, with direct multiplication of the corresponding t-section of the main bridge by an appropriate coefficient k < 1.

At the left low corner of each slide, the corresponding instant is presented. The neighbor slides with the same instant differ from each other by the point of view. In passage from one instant to the next, the point of view does not change.

Patsko sector homepage