Литература

1

Jackson D. On approximation by trigonometric sums and polynomials // Trans. Amer. Math. Soc. 1912. V. 13. P. 491-515.

2

Ахиезер Н.И. Лекции по теории аппроксимации. М.: Гостехиздат, 1947. 323 с.

3

Стечкин С.Б. О порядке наилучших приближений непрерывных функций // Изв. АН СССР, серия матем., 1951. Т. 15. С. 219-242.

4

Тиман А.Ф. Теория приближения функций действительного переменного. М.: Физматгиз, 1960. 624 с.

5

Никольский С.М. Приближение функций многих переменных и теоремы вложения. М.: Наука, 1969. 480 с.

6

Корнейчук Н.П. Точная константа в теореме Д. Джексона о наилучшем равномерном приближении непрерывных периодических функций // Докл. АН СССР. 1962. Т. 145, N 3. С. 514-515.

7

Черных Н.И. О неравенстве Джексона в 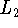// Труды МИ АН СССР. 1967. Т. 88. С. 71-74.

8

Черных Н.И. О наилучшем приближении периодических функций тригонометрическими полиномами в 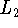// Матем. заметки. 1967. Т. 2, вып. 5. С. 513-522.

9

Бабенко А.Г. Точное неравенство Джексона - Стечкина в пространстве 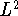функций на многомерной сфере // Матем. заметки. 1996. Т. 60, вып. 3. С. 333-355.

10

Юдин В.А. Многомерная теорема Джексона в 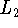// Матем. заметки. 1981. Т. 29, N 2. С. 309-315.

11

Йон Ф. Плоские волны и сферические средние в применении к дифференциальным уравнениям с частными производными. М.: Изд-во ИЛ, 1958. 158 с.

12

Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. Минск: Наука и техника, 1987. 688 с.

13

Попов В.Ю. О точных константах в неравенствах Джексона для наилучших сферических среднеквадратичных приближений // Известия вузов. Математика. 1981. Т. 12. С. 67-78.

14

Попов В.Ю. Среднеквадратичные приближения дифференцируемых функций многих переменных // Исследования по функциональному анализу и его приложениям. Сборник научных трудов. Свердловск: изд-во Уральского гос. ун-та, 1985. С. 92-102.

15

Попов В.Ю. Многомерные приближения в 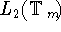// Теория функций и приближений. Труды 3-й Саратовской зимней школы (27 января - 7 февраля 1986 г.). Межвузовский научный сборник. Часть 3. Саратов: Изд-во Саратовского ун-та, 1988. С. 22-25.

16

Стейн И., Вейс Г. Введение в гармонический анализ на евклидовых пространствах. М.: Мир, 1974. 336 с.

17

Ронкин Л.И. Введение в теорию целых функций многих переменных. М.: Наука, 1971. 430 с.

18

Попов В.Ю. О наилучших среднеквадратических приближениях функций m переменных // Матем. заметки. 1973. Т. 14, вып. 6. С. 913-924.

19

Рустамов Х.П. О приближении функций на сфере // Известия Академии наук, серия матем., 1993. Т.  57, N 5. С. 127-148.

20

Arestov V.V., Chernykh N.I. On the 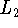-approximation of periodic functions by trigonometric polynomials // Approximation and functions spaces. Proc. Conf. Gdan'sk, 1979. Amsterdam: North-Holland, 1981. P. 25-43.

21

Logan B.F. Extremal problems for positive-definite bandlimited functions. II. Eventually negative functions // Siam. J. Math. Anal. 1983. V. 14, N 2. P. 253-257.

22

Ибрагимов И.И., Насибов Ф.Г. Об оценке наилучшего приближения суммируемой функции на вещественной оси посредством целых функций конечной степени // Докл. АН СССР. 1970. Т. 194, N 5. С. 1013-1016.

23

Попов В.Ю. О наилучших среднеквадратических приближениях целыми функциями экспоненциального типа // Известия вузов. Математика. 1972. N 6. С. 65-73.

24

Арестов В.В., Попов В.Ю. Неравенство Джексона на сфере в 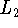// Известия вузов. Математика. 1995. N 8. С. 13-20.

25

Ватсон Г.Н. Теория бесселевых функций. Часть первая. М.: изд-во Иностранной литературы, 1949. 798 с.

26

Бейтмен Г., Эрдейи А.И. Высшие трансцендентные функции. Т. 2. Функции Бесселя. М.: Наука, 1966. 295 с.

27

Шилов Г.Е. Математический анализ. Специальный курс. М.: Гос. изд-во Физ.-мат. лит., 1960. 388 с.

28

Левитан Б.М. Разложение по функциям Бесселя в ряды и интегралы Фурье // Успехи матем. наук. 1951. Т. 6, вып. 2. С. 102-143.

29

Сонин Н.Я. Исследования о цилиндрических функциях и специальных полиномах. М.: Гостехиздат, 1954. 244 с.

30

Шалаев В.В. О поперечниках в 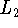классов дифференцируемых функций, определяемых модулями непрерывности высших порядков // Украинский матем. журн., 1991. Т. 43, N 1. С. 125-129.