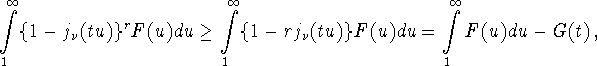
причем функция G принадлежит множеству
Для доказательства утверждения (А) теоремы 1 применим лемму 1 и рассуждения аналогичные тем, которые приведены в работе автора [9]. Для доказательства утверждения (В) теоремы 1 достаточно использовать методику, разработанную В.В.Арестовым в работах [24, п. 3,], [9, лемма 4.2,], с учетом известных свойств (21), (22) нормированных функций Бесселя.
Подробнее, пусть ![]() , в силу неравенства
, в силу неравенства ![]() при
при ![]() , для любой функции F из
класса
, для любой функции F из
класса ![]() (см. (31)), имеем
(см. (31)), имеем
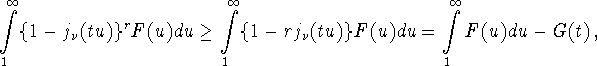
причем функция G принадлежит множеству ![]() ,
определенного формулой (55). Отсюда, леммы 1 и равенств
(35), (46) следует первое неравенство утверждения
(А) теоремы 1. Второе неравенство утверждения (А) доказывается
аналогично.
,
определенного формулой (55). Отсюда, леммы 1 и равенств
(35), (46) следует первое неравенство утверждения
(А) теоремы 1. Второе неравенство утверждения (А) доказывается
аналогично.
Для доказательства утверждения (В) теоремы 1 воспользуемся
равенством (46) и тем фактом, что величина
![]() (см.(31)), являющаяся точной
константой в неравенстве (30), совпадает с точной
константой в неравенстве
(см.(31)), являющаяся точной
константой в неравенстве (30), совпадает с точной
константой в неравенстве
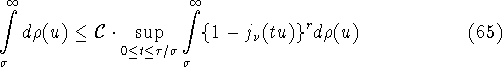
при ![]() на множестве всех неубывающих
функций
на множестве всех неубывающих
функций ![]() , имеющих ограниченную вариацию на полуоси
, имеющих ограниченную вариацию на полуоси
![]() . Теперь для доказательства, того что точная
константа в этом неравенстве не меньше единицы, зафиксируем
произвольную неограниченную последовательность U чисел
. Теперь для доказательства, того что точная
константа в этом неравенстве не меньше единицы, зафиксируем
произвольную неограниченную последовательность U чисел
![]() Затем по схеме В.В.Арества (см.
[9, лемма 4.2,]), с учетом свойств (21),
(22) нормированных функций Бесселя, построим искомую
последовательность
Затем по схеме В.В.Арества (см.
[9, лемма 4.2,]), с учетом свойств (21),
(22) нормированных функций Бесселя, построим искомую
последовательность ![]() неубывающих ступенчатых
функций ограниченной вариации с разрывами в U. Теорема 1 доказана.
неубывающих ступенчатых
функций ограниченной вариации с разрывами в U. Теорема 1 доказана.
Семинар профессора В.В.Арестова в Уральском госуниверсите при участии доцента В.Ю.Попова оказал значительное влияние на исследования автора.
Поступила 09.01.97