ДЛЯ L2-ПРИБЛИЖЕНИЙ НА
ПОЛУПРЯМОЙ С ВЕСОМ ЛАГЕРРА
Статья опубликована в сборнике:
Труды международной школы С.Б.Стечкина по теории функций (Россия, г.Миасс Челябинской обл., 24 июля - 3 авг. 1998 г.). Екатеринбург: УрO РАН, 1999. С. 38-63. Библиогр.: 33 назв.
Данная работа посвящена изучению точной константы в неравенстве Джексона-Стечкина между наилучшим среднеквадратичным приближением произвольной комплексной функции на полупрямой с весом Лагерра tae-t,I>a > - 1/2, алгебраическими многочленами заданной степени с одной стороны и ее модулем непрерывности вещественного порядка r > 0, порожденного обобщенным сдвигом (см. [1]), построенном на основе ряда Фурье-Лагерра функции с другой стороны. Интегральное представление указанного сдвига может быть получено с помощью формулы умножения для многочленов Лагерра, которую установили Харди (при a = 0) и Ватсон (при a > - 1/2) [2]. Соответствующие прямые и обратные теоремы теории приближения исследовались в работах [3]-[7], а в статье [8] указанные теоремы установлены в терминах модуля непрерывности, построенного на основе нового оператора обобщенного сдвига.
В этой заметке найдено наименьшее значение точной
константы в неравенстве Джексона-Стечкина с
(обобщенным) модулем непрерывности порядка r![]() 1 и
локализована точка, начиная с которой указанная константа
(как функция аргумента модуля непрерывности) выходит на
свой минимум, равный единице. Содержащиеся здесь
результаты, частично, анонсированы автором в
[9].
1 и
локализована точка, начиная с которой указанная константа
(как функция аргумента модуля непрерывности) выходит на
свой минимум, равный единице. Содержащиеся здесь
результаты, частично, анонсированы автором в
[9].
Первые точные результаты в прямых теоремах теории приближения функций одной и нескольких переменных получили Н.П.Корнейчук [10], [11], Н.И.Черных [12]-[14], В.А.Юдин [15]. Более подробная история этого вопроса и информация о дальнейшем развитии темы о точных неравенствах Джексона-Стечкина на некоторых классических многообразиях содержится в [16]. Среди последних работ в этом направлении отметим [17]-[24].
Введение.
Рассмотрим пространство
L2 = L2a = L2(![]() +, tae-t), a > - 1, комплексных функций, измеримых
по Лебегу на полуоси
+, tae-t), a > - 1, комплексных функций, измеримых
по Лебегу на полуоси
![]() + = [0, +
+ = [0, + ![]() ), квадрат
модуля которых суммируем с весом tae-t на
), квадрат
модуля которых суммируем с весом tae-t на
![]() +. Это пространство наделено скалярным произведением
и нормой
+. Это пространство наделено скалярным произведением
и нормой
С настоящего момента мы будем рассматривать лишь случай
a![]() - 1/2. Как обычно, через
C[
- 1/2. Как обычно, через
C[![]() ,
,![]() ]
будем обозначать пространство вещественных функций,
непрерывных на отрезке
[
]
будем обозначать пространство вещественных функций,
непрерывных на отрезке
[![]() ,
,![]() ] с равномерной нормой
] с равномерной нормой
На основе разложения (1.6) функции f ![]() L2 в ряд
Фурье-Лагерра определим ее (обобщенный) модуль
непрерывности порядка r > 0 (не обязательно целого) в точке
L2 в ряд
Фурье-Лагерра определим ее (обобщенный) модуль
непрерывности порядка r > 0 (не обязательно целого) в точке
![]()
![]() 0, положив
0, положив
Оператором обобщенного сдвига с шагом h > 0 называют оператор Th, действующий в пространстве L2 по правилу [1]
Видно, что оператор Th является линейным, кроме того, из предложения 1.1, следует его ограниченность как оператора из L2a в L2a, aФункцией Бесселя первого рода индекса q (см. [26, § 3.1, формула (8)], [25, формула (1.71.1)]) называется функция
Положим
Пусть
1![]() p
p![]()
![]() , a > - 1/2, обозначим через Lpa
пространство комплексных функций, измеримых по Лебегу на полуоси
, a > - 1/2, обозначим через Lpa
пространство комплексных функций, измеримых по Лебегу на полуоси
![]() + с конечной нормой
+ с конечной нормой
При a![]() - 1/2 обозначим через
- 1/2 обозначим через ![]() (a) наибольшее
неотрицательное число, удовлетворяющее условию
(a) наибольшее
неотрицательное число, удовлетворяющее условию
Для фиксированных
![]() > 0, n
> 0, n ![]()
![]() , r > 0, a
, r > 0, a![]() - 1/2 рассмотрим задачу о точной константе
K = K(
- 1/2 рассмотрим задачу о точной константе
K = K(![]() , n, r, a) в неравенстве Джексона-Стечкина
, n, r, a) в неравенстве Джексона-Стечкина
В работах [3]-[7] оператор сдвига Th применялся, в частности, для построения модуля непрерывности и доказательства соответствующих прямых и обратных теорем теории приближения. Известно [3]-[7], что величина K(n-1, n, 2, a) ограничена по n при каждом фиксированном a > - 1/2.
Для
![]() > 0, n
> 0, n ![]()
![]() , r > 0, a
, r > 0, a![]() - 1/2,
наряду с задачей (1.17), рассмотрим задачу о точной константе
æ = æ(
- 1/2,
наряду с задачей (1.17), рассмотрим задачу о точной константе
æ = æ(![]() , n, r, a) в неравенстве
, n, r, a) в неравенстве
В.В.Арестов получил довольно общий результат [31, лемма 3] , [16, лемма 4.2] (см. ниже лемму 2.2), из которого следует оценка снизу
при
В данной заметке указана некоторая область изменения параметров
![]() , n, r, a, при которых неравенство (1.22) обращается в
равенство. Для точной формулировки результата нам необходимы
следующие обозначения:
, n, r, a, при которых неравенство (1.22) обращается в
равенство. Для точной формулировки результата нам необходимы
следующие обозначения:
Относительно jq известны следующие утверждения (см. [26, §15.2, §15.6]):
Напомним, что из общих свойств ортогональных многочленов
(см. [25, теорема 3.3.2]) и верхней оценки в
(1.23) следует, что
![]() , строго убывая,
стремится к нулю при возрастании n к бесконечности.
Поэтому для каждого числа a > - 1/2 существует минимальное
натуральное число n = n(a), начиная с которого
выполняется неравенство:
2
, строго убывая,
стремится к нулю при возрастании n к бесконечности.
Поэтому для каждого числа a > - 1/2 существует минимальное
натуральное число n = n(a), начиная с которого
выполняется неравенство:
2![]()
![]() ja - 1/2, т.е.
ja - 1/2, т.е.
Основным результатом данной работы являются оценки сверху величины (1.17), которые выполняются при a > - 1/2
Теорема 1.1. Пусть a > - 1/2. Тогда на множестве функций
f ![]() L2a, отличных от постоянной, справедливы
неравенства
L2a, отличных от постоянной, справедливы
неравенства
Причем, в случае r![]() 1 множитель 1, стоящий перед модулем
непрерывности в неравенстве (1.25), нельзя заменить на
меньший.
1 множитель 1, стоящий перед модулем
непрерывности в неравенстве (1.25), нельзя заменить на
меньший.
Для доказательства неравенств (1.25), (1.26) используются идеи, содержащиеся в работах Н.И.Черных [12], [13] и В.А.Юдина [15], а также схема работы автора [16]. Последнее утверждение теоремы 1.1 следует из неравенства (1.22).
В пункте 4 приводится доказательство теоремы 1.1, которое основано на утверждениях предыдущих пунктов. Пункт 5 посвящен неравенству Джексона-Стечкина со смешанным обобщенным модулем непрерывности. В заключении данного пункта, отметим, что в случае a = - 1/2 задача (1.17) остается открытой.
2. Оценка снизу. Вначале приведем несколько утверждений, которые являются следствиями известных свойств многочленов Лагерра.
Из явного выражения (1.2) и неравенства (1.4)
для стандартизованных многочлена Лагерра следует, что
многочлены (1.3), наряду со свойством: Rk(0) = 1,
k ![]()
![]() + , обладают свойством:
Rk'(0) < 0, k
+ , обладают свойством:
Rk'(0) < 0, k ![]()
![]() , a
, a![]() - 1/2. Поэтому при a
- 1/2. Поэтому при a![]() - 1/2
числа
- 1/2
числа
Теорема 2.1. Пусть a - произвольное вещественное число и n - произвольное натуральное число. Последовательность, образованная относительными максимумами функции | Ln(a)(x)| и значением этой функции в точке x = 0, является убывающей при x < a + 1/2 и возрастающей при x > a + 1/2.
Из этой теоремы, предложения 1.1 и равенства (2.1) вытекают
следующие утверждения
для величины ![]() (a)
(a)
Отсюда следует такое утверждение
Лемма 2.1. Пусть
a![]() - 1/2, r > 0,
- 1/2, r > 0, ![]() > 0, n
> 0, n ![]()
![]() . Тогда функции
. Тогда функции
Кроме того, если a > - 1/2, то при любом
![]()
![]() (0,
(0,![]() ]
выполняется соотношение:
]
выполняется соотношение:
![]() | Pk|C[
| Pk|C[![]() ,
,![]() ] = 1.
] = 1.
Для более общих систем функций В.В.Арестов [16, лемма 4.2] доказал следующее утверждение (двойственный аналог которого доказан им ранее в [31, лемма 3]).
Лемма 2.2. Пусть на отрезке
[0,![]() ],
], ![]() > 0, задана
система непрерывных вещественных функций Fk,
k = 0, 1, 2,..., удовлетворяющая условиям:
Fk(0) = 0,
k
> 0, задана
система непрерывных вещественных функций Fk,
k = 0, 1, 2,..., удовлетворяющая условиям:
Fk(0) = 0,
k ![]()
![]() + ; существует
абсолютная константа
1
+ ; существует
абсолютная константа
1![]() M <
M < ![]() такая, что
| Fk(t)|
такая, что
| Fk(t)|![]() M при 0
M при 0![]() t
t![]()
![]() , k
, k ![]()
![]() + ; для любого числа
+ ; для любого числа
![]()
![]() (0,
(0,![]() ] выполняется соотношение
] выполняется соотношение
Следствие 2.1. Если
a > - 1/2, r > 0, ![]() > 0, n
> 0, n ![]()
![]() , то существует последовательность
функций
fl, l = 1, 2, 3,..., из L2a такая, что
, то существует последовательность
функций
fl, l = 1, 2, 3,..., из L2a такая, что
Д о к а з а т е л ь с т в о. Рассмотрим систему функций
 Rn + k(t)
Rn + k(t) Следствие 2.1 влечет оценку (1.22) для величины (1.17).
3. Вспомогательные утверждения.
Лемма 3.1. Пусть
a > - 1/2, 0 < 2![]()
![]() ja - 1/2, функция F неотрицательна и непрерывна на
ja - 1/2, функция F неотрицательна и непрерывна на
![]() +, кроме того, ее носитель сосредоточен на полуинтервале
[0,
+, кроме того, ее носитель сосредоточен на полуинтервале
[0,![]() ), т.е. F(t) = 0 при t
), т.е. F(t) = 0 при t![]()
![]() . Тогда функция
F
. Тогда функция
F![]() (t) = T
(t) = T![]() F(t) является неотрицательной и непрерывной на
F(t) является неотрицательной и непрерывной на
![]() + с носителем на
[0, 4
+ с носителем на
[0, 4![]() ), т.е.
F
), т.е.
F![]() (t) = 0 при
t
(t) = 0 при
t![]() 4
4![]() .
.
Д о к а з а т е л ь с т в о. вытекает из определения
(1.13) сдвига и следующих двух легко проверяемых неравенств
| при | t |
||
| 0 |
при | 0 < |
|
| 0 |
|||
| при | 0 |
Как уже отмечалось в первом пункте статьи, следствием результата (1.12) Харди и Ватсона является интегральное представление (1.13) для оператора сдвига Th. Кроме того, из определения (1.9) вытекает свойство самосопряженности оператора сдвига Th (см. [6]).
Лемма 3.2. Пусть
a![]() - 1/2, h
- 1/2, h![]() 0. Тогда
для любых двух функций f, g из L2a выполняется
равенство
0. Тогда
для любых двух функций f, g из L2a выполняется
равенство
Рассмотрим следующее множество
Gn = Gn, a, n ![]()
![]() ,
a
,
a![]() - 1/2 функций, заданных на
- 1/2 функций, заданных на
![]() +
+
Важной характеристикой системы многочленов Лагерра является точка Черных множества Gn, которая определяется следующим образом
Определение 3.1. Положительное число
![]() =
= ![]() (Gn) называется точкой Черных для множества
Gn, если одновременно выполняются следующие два условия
(Gn) называется точкой Черных для множества
Gn, если одновременно выполняются следующие два условия
(а) для любой функции f из Gn найдется точка
x* = x*(f ) из
открытого интервала
(0,![]() ), в которой f (x*) < 0;
), в которой f (x*) < 0;
(b) для любого числа
![]()
![]() (0,
(0,![]() ) существует функция
f
) существует функция
f![]()
![]() Gn
и число
Gn
и число
![]() > 0 такие, что
f
> 0 такие, что
f![]() (x)
(x)![]()
![]() при всех
x
при всех
x ![]() [0,
[0,![]() ].
].
Первые результаты, связанные с такой же характеристикой системы косинусов, принадлежат Н.И.Черных. Он доказал [12], [14] утверждения , которые эквивалентны равенству
Напомним (см. (1.24)), что для a > - 1/2 через n(a) мы обозначили минимальное натуральное число n, начиная с которого выполняется неравенство: Основным результатом этого пункта является
Лемма 3.3. Пусть a > - 1/2. Тогда для точки Черных множества Gn справедливы оценки
Д о к а з а т е л ь с т в о. Оценка снизу (3.2) вытекает из того, что функция Rn принадлежит Gn и удовлетворяет неравенству
Доказательство оценки сверху (3.3) будем проводить
по схеме Н.И.Черных [12] . Именно,
построим вес - неотрицательную, ненулевую и интегрируемую
на отрезке
[0, 4![]() ] функцию
v(x) = vn, a(x),
удовлетворяющую условиям
] функцию
v(x) = vn, a(x),
удовлетворяющую условиям
Идея построения искомого веса v близка к той, которая применялась В.А.Юдиным в работе [15]. Положим
Искомый вес v определим по формуле
Таким образом, мы нашли вес v, удовлетворяющий условиям (3.4), что завершает доказательства леммы 3.3.
В дальнейшем нам понадобится очевидное
Предложение 3.1. Имеют место следующие неравенства
4. Д о к а з а т е л ь с т в о. теоремы 1.1.
Рассмотрим случай r![]() 1. Докажем неравенство (1.25). В
силу (1.8), (1.19), (1.21) и предложения 3.1
нам достаточно установить неравенство
1. Докажем неравенство (1.25). В
силу (1.8), (1.19), (1.21) и предложения 3.1
нам достаточно установить неравенство
Неравенство (1.26) доказывается аналогично. Следствие 2.1. влечет последнее утверждение теоремы 1.1, чем и завершается ее доказательство теоремы 1.1.
5. Неравенство Джексона-Стечкина со смешанным обобщенным модулем непрерывности. В последнее время возрос интерес к прямым и обратным теоремам теории приближения в терминах смешанного обобщенного модуля непрерывности, основанного на операторе обобщенного сдвига, который строится с помощью двух различных систем функций (система функций, определяющая сдвиг, отличается от ортогональной системы функций, задающей базис гильбертова пространства). Так в совместной работе М.К.Потапова и С.К.Танкаевой [8] был введен новый оператор обобщенного сдвига, который в гильбертовом случае можно задать с помощью двух систем многочленов Лагерра с различными показателями.
Подробнее. Для вещественной неубывающей на полуоси
![]() +
функции
+
функции ![]() обозначим через
L2(
обозначим через
L2(![]() +, d
+, d![]() ) пространство
комплексных функций со скалярным произведением и нормой
) пространство
комплексных функций со скалярным произведением и нормой
Обозначим через ![]() множество всех полиномов
p(t) = c0
множество всех полиномов
p(t) = c0![]() (t) + c1
(t) + c1![]() (t) +...+ cn
(t) +...+ cn![]() (t) с
комплексными коэффициентами
c0, c1,..., cn. Наилучшим
приближением функции f из
L2(
(t) с
комплексными коэффициентами
c0, c1,..., cn. Наилучшим
приближением функции f из
L2(![]() +, d
+, d![]() ) множеством
) множеством
![]() называют величину
называют величину
Приведем один конкретный пример оператора смешанного обобщенного
сдвига, построенного в [8], для которого
имеется изящное интегральное представление. Именно, в работе
[8] был введен новый оператор обобщенного
сдвига, действующий в пространстве Lp![]() (см. 1.14) по
закону
(см. 1.14) по
закону
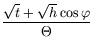 .
.