В данной работе на основе понятия сферического сдвига или,
что то же самое, сферического среднего (см. [11, гл. 1, 4,])
по схеме Грюнвальда - Летникова (см. [12, § 20,])
определяется разностный оператор порядка r>0 (необязательно целого)
с шагом 
, а с помощью него - соответствующий
модуль непрерывности комплексной функции 
,
в терминах которого затем ставится задача о точной константе в неравенстве
Джексона - Стечкина для наилучших приближений
в пространстве 
классом 
целых функций из экспоненциального
сферического типа 
С помощью известных рассуждений,
которые использовались, к примеру,
В.Ю.Поповым в работах [13] - [15],
указанная выше многомерная задача сводится (см. пункт 2 ниже) к одномерной
задаче, в свою очередь, последняя задача эквивалентна (см. пункт 3 ниже)
задаче о
точном неравенстве Джексона - Стечкина в пространстве
вещественных измеримых функций на полуоси
суммируемых с квадратом с весом 
Итак, пусть 
есть гильбертово пространство
комплексных функций на 
с обычным скалярным произведением
и нормой
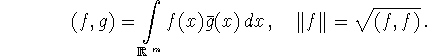
В дальнейшем мы будем часто использовать
преобразование Фурье
функции 
определив его стандартным образом формулой (см. [16])
здесь 
-
скалярное произведение векторов x,y из 
Функцию 
можно выразить через ее
преобразование Фурье 
по формуле
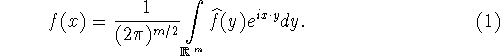
Для преобразований Фурье в пространстве 
имеет место формула Планшереля
Обозначим через класс целых функций
экспоненциального сферического типа 
принадлежащих пространству
(см. [5, § 3.2.6,], [17, гл. 3, § 4,], [18]).
Класс состоит из функций 
носитель
преобразования Фурье которых
лежит в евклидовом шаре
радиуса 
с центром в начале координат пространства
Наилучшим приближением функции f из классом
называется величина
Сферический сдвиг с шагом или, что то же самое,
сферическое среднее (см. [11, гл. 4, стр. 72,]) есть
оператор 
действующий по правилу
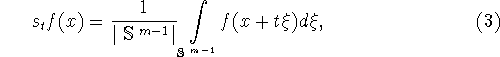
где 
- единичная евклидова сфера
в 
а
- площадь ее поверхности. В случае m=1
единичная сфера 
состоит из двух точек -1,1 и под
ее мерой мы понимаем число 2. Таким образом, оператор 
в
этом случае приобретает вид 
Известно, что норма оператора как
оператора из в 
равна единице
(см., например, формулу (27) ниже). Поэтому можно применить
конструкцию Грюнвальда - Летникова (см. [12, § 20,]) для построения
разностного оператора порядка r>0 (не обязательно целого).
А именно, разностным оператором порядка r>0 с шагом
называется оператор
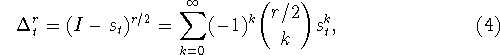
где I есть тождественный оператор и 
. Для функции ее
модулем непрерывности порядка r>0 называется следующая функция
аргумента 
Для функций, заданных на многомерной сфере соответствующие разностные операторы и модули непрерывности дробного порядка рассматривал Х.П.Рустамов [19].
В данной работе изучается задача о точной константе 
в неравенстве Джексона - Стечкина
Наименьшую константу в этом неравенстве можно представить в виде
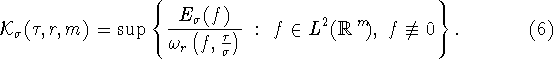
Нетрудно показать, что величина 
не зависит от
в следующем пункте будет дано краткое доказательство этого
утверждения.
Перейдем к изложению известных результатов, относящихся к задаче о точной константе (6) в неравенстве (5). Авторы приводимых ниже результатов применяют другие модули непрерывности, но при доказательстве они переходят к задачам, которые возникают и в данной работе. Мы приведем указанные результаты в принятых здесь обозначениях.
Начнем с одномерного случая. И.И.Ибрагимов и Ф.Г.Насибов [22] получили такое утверждение
Теорема A ([22]).
Для произвольного и любой функции 
справедливы неравенства
Следующий результат был независимо от предыдущего доказан В. Ю. Поповым [23].
Теорема B ([23]).
Пусть Тогда для каждой ненулевой функции 
выполняются неравенства
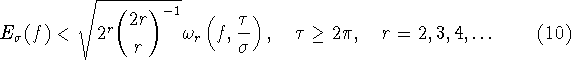
Эти неравенства являются точными, т.е. для величины 
в
одномерном случае (m=1) справедливы равенства
при 
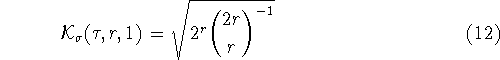
при 
Этот факт следует из результатов
Н.И.Черныха [7], [20]
о найменьшем значении аргумента модуля непрерывности
(первого порядка), начиная с которого точная
константа в неравенстве Джексона в пространстве 
выходит на
свой минимум. Утверждение (13) вытекает также из более
позднего результата Логана [21].
Перейдем к многомерному случаю. В.Ю.Попов [13] доказал, что
Как уже было отмечено выше, В.А.Юдин [10] установил точное
неравенство Джексона между наилучшим среднеквадратичным приближением
функции на многомерном торе 
тригонометрическими
полиномами заданного сферического порядка и ее классическим модулем
непрерывности первого порядка определяемого с помощью выпуклого,
замкнутого, центрально симметричного тела. При доказательстве этого
неравенства он, фактически, получил родственный результат в пространстве
. В частном случае когда указанное выше тело является
евклидовым шаром, из результата В.А.Юдина можно вывести равенство
где
- первый положительный нуль функции Бесселя
индекса 
(см. формулу (19) ниже).
Собственно понимание того, как указанный вывод можно осуществить, позволило
автору данной работы получить оценку
которая вместе с оценкой снизу
вытекающей из результата В.В.Арестова [24, п. 3,],
[9, лемма 4.2,], влечет решение задачи (6) при наложенных
в (16) ограничениях, а именно, что
Это утверждение и является основным результатом настоящей работы.
Отметим еще, что из работ [13] - [15] следует
решение задачи (6) о вычислении величины для 
при
"малых" 
Подробнее, пусть 
минимальное положительное значение аргумента нормированной функции
Бесселя 
(см. формулы (20), (19) ниже), при котором
она достигает локального минимума, обозначим через 
, а минимальное
положительное значение аргумента функции , при котором достигается
ее локальный максимум, обозначим через 
. Единственный корень
уравнения
обозначим через
Тогда для любых
имеет место равенство
В одномерном случае (m=1) к настоящему времени нет ни одной точки из
области 
при которой была бы найдена величина
