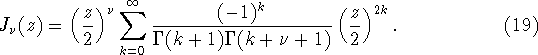
Нормированной функцией Бесселя индекса
Как известно (см. [25]; § 7.3, стр. 23, формула (4) и § 7.13, стр. 98, формула (3) в [26]), она обладает следующими свойствами
Приведем два важных примера таких функций
Функция Бесселя индекса ![]() определяется так
(см. стр. 51, формула (8) в [25],
стр. 12, формула (2) в [26])
определяется так
(см. стр. 51, формула (8) в [25],
стр. 12, формула (2) в [26])
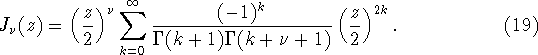
Нормированной функцией Бесселя индекса ![]() называется функция
называется функция
![]()
Как известно (см. [25]; § 7.3, стр. 23, формула (4) и
§ 7.13, стр. 98, формула (3) в [26]),
она обладает следующими свойствами
![]()
![]()
Приведем два важных примера таких функций
![]()
С помощью формулы Планшереля (2)
нетрудно убедится, что величина наилучшего приближения
функции ![]() классом
классом ![]() выражается через
преобразование Фурье
выражается через
преобразование Фурье ![]() функции f формулой
функции f формулой
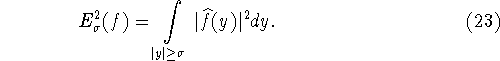
Зафиксируем произвольный вектор ![]() и положим
и положим
![]() Известно (см. гл. 4, стр. 72, формулы (4.1)-(4.4) в [11]),
что оператор
Известно (см. гл. 4, стр. 72, формулы (4.1)-(4.4) в [11]),
что оператор
![]() сферического сдвига с шагом
сферического сдвига с шагом ![]() (см. (3))
действует на функцию
(см. (3))
действует на функцию ![]() следующим образом
следующим образом
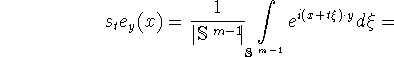
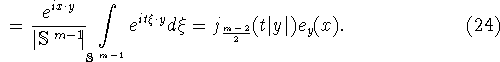
На последнем шаге в (24) мы воспользовались известными соотношениями
для усреднения экспоненты по сфере (см. [11, гл. 1, стр. 15-16,],
[16], [27, гл. 3, § 8,], [13]).
Таким образом, для функции ![]() имеем, окончательно, формулу
имеем, окончательно, формулу
![]()
Применив k раз к обеим частям равенства (1) оператор сферического
сдвига и воспользовавшись соотношением (25), получим
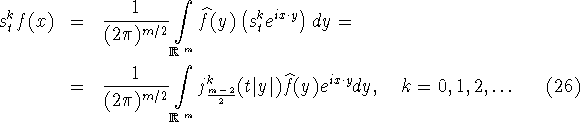
Это соотношение в силу свойства (21), влечет равенство
единице нормы оператора ![]() (как оператора
из
(как оператора
из ![]() в
в ![]() )
при любых
)
при любых ![]() в частности (при k=1) имеем
в частности (при k=1) имеем
![]()
Исходя из определения (4) разностного оператора,
с помощью формулы (26) получим представление
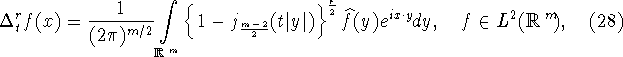
для любых
![]() Отсюда в силу формулы Планшереля следует, что
Отсюда в силу формулы Планшереля следует, что
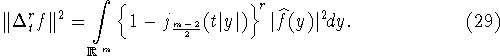
Формулы (29) и (23) сводят многомерную
задачу (6) к одномерной экстремальной задаче
о точной константе
![]() в неравенстве
в неравенстве
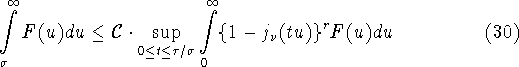
при ![]()
![]() на множестве всех неотрицательных функций
на множестве всех неотрицательных функций ![]() (верхняя грань по множеству
(верхняя грань по множеству ![]() в правой части (30) заменена на верхнюю грань
по множеству
в правой части (30) заменена на верхнюю грань
по множеству ![]() исходя из свойства четности нормированной функции Бесселя
исходя из свойства четности нормированной функции Бесселя ![]() ).
Для точной константы
).
Для точной константы ![]() в неравенстве
(30) справедлива формула
в неравенстве
(30) справедлива формула
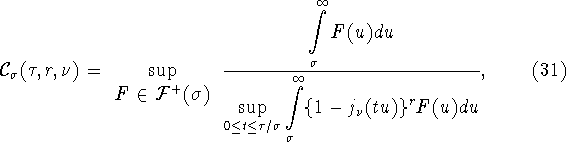
где
![]()
есть множество функций ненулевых, неотрицательных и суммируемых на полуоси
![]() .
При этом константы (6) и (31) связаны соотношением
.
При этом константы (6) и (31) связаны соотношением
![]()
для ![]()
Убедимся, что величина
![]() не зависит от
не зависит от ![]() В интегралах, участвующих в (31), произведем замену переменных
В интегралах, участвующих в (31), произведем замену переменных
![]() В результате получим
В результате получим
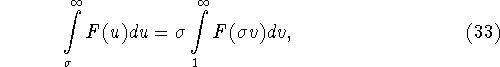
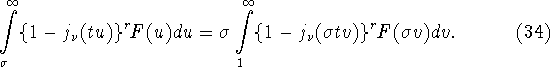
Для функции ![]() рассмотрим функцию
рассмотрим функцию
![]() ясно, что
ясно, что
![]() Построенное отображение осуществляет
взаимно однозначное соответствие между множествами
Построенное отображение осуществляет
взаимно однозначное соответствие между множествами
![]() и
и ![]() Поэтому имеем
Поэтому имеем
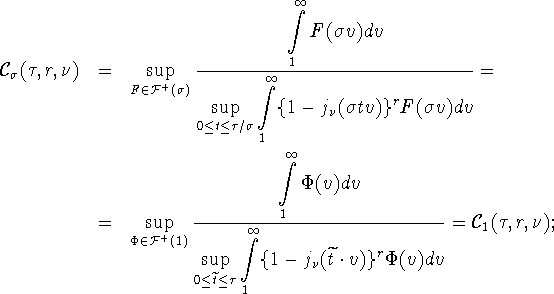
здесь была введена новая переменная ![]() Таким образом,
принимая во внимание равенство (32), получаем, что при
Таким образом,
принимая во внимание равенство (32), получаем, что при
![]() выполняются равенства
выполняются равенства
![]()
![]()