0.

В данной работе изучается линейная экстремальная задача для непрерывных на отрезке функций, представимых рядами по ортогональным многочленам, с ограничениями на значения функций и коэффициенты разложений. К задачам такого типа сводятся экстремальные задачи различных разделов математики. Здесь обсуждается вариант этой задачи, возникший в исследованиях Ф.Дельсарта [1], [2] границ упаковок в некоторых метрических пространствах. Схема Дельсарта была развита и успешно применена в работах Г.А.Кабатянского и В.И.Левенштейна [3], Э.Одлыжко и Н.Слоэна [4], В.И.Левенштейна [5], [6], В.М.Сидельникова [7] в связи с исследованием упаковок метрических пространств и, в частности, контактных чисел евклидовых пространств ${\bf R}^m$. Изложение этих результатов и другая родственная, богатая информация имеется в монографии Дж.Конвея и Н.Слоэна [8]. Из последних работ на эту тему следует сказать о работе В.А.Юдина [9], в которой был разработан аналог схемы Дельсарта [1] - [8] для изучения достаточно общей задачи минимизации функции фиксированного числа точек на единичной сфере евклидова пространства ${\bf R}^m;$ исследования В.А.Юдина [9] были продолжены в [10], [11].

Контактным числом пространства ${\bf R}^m,\ m\ge 2,$ называют максимальное число шаров единичного радиуса с непересекающимися внутренностями, касающихся единичного шара пространства; это число в дальнейшем будет обозначаться через $\tau_m.$ Задача исследования контактных чисел имеет большую историю (см. [8], [12]). В настоящее время точное значение $\tau_m$ известно лишь при $m=2,3,8,24,$ а именно, $\tau_2=6, \tau_3=12, \tau_8=240, \tau_{24}=196560;$ в остальных случаях вопрос о точных значениях $\tau_m$ открыт. Для произвольных значений $m$ известны оценки снизу и сверху константы $\tau_m$; так в четырехмерном случае

$$24\le \tau_4\le 25.$$ (0.1)

Однако эти оценки не дают, к примеру, порядка поведения контактного числа $\tau_m$ по $m.$

Задачу о контактном числе пространства ${\bf R}^m$ можно сформулировать (см., например, [8, гл.1, §2]) в терминах экстремальной задачи для подмножеств (называемых в данной тематике сферическими кодами) единичной сферы ${\bf S}={\bf S}^{m-1}\subset {\bf R}^m.$ Пусть ${\cal B}$ есть некоторое множество шаров единичного радиуса пространства ${\bf R}^m$ с непересекающимися внутренностями, которые касаются единичного шара (с центром в начале координат) пространства. Обозначим через $W=W({\cal B})$ множество точек единичной сферы ${\bf S}$ (или, то же самое, единичных векторов пространства), являющихся проекциями на сферу ${\bf S}$ центров шаров $B\in {\cal B};$ ясно, что $W$ состоит из точек, в которых шары $B\in {\cal B}$ касаются сферы ${\bf S}$. Множество $W\subset {\bf S}$ характеризуется тем свойством, что (плоский) угол между любыми двумя различными векторами $x,y\in W$ будет не меньше, чем $\frac{\pi}{3},$ а это означает, что скалярное произведение $xy$ любых двух векторов $x, y\in W, x\ne y,$ удовлетворяет условию $xy\le \frac{1}{2}.$ Таким образом, контактное число $\tau_m$ равно наибольшему значению мощности множества $W\subset {\bf S}$ со свойством

$$-1\le xy\le \frac{1}{2},\quad x, y\in W, x\ne y.$$ (0.2)

Оценки снизу контактных чисел дают конкретные сферические коды со свойством (0.2). Построение экстремальных (или близких к экстремальным) сферических кодов есть интересный и трудный раздел дискретной геометрии, связанный со многими разделами математики. В данной работе вопрос об оценках снизу не обсуждается. Исторические сведения и результаты на эту тему можно найти в монографии [8].

Лучшие оценки сверху контактных чисел получены в работах Г.А.Кабатянского и В.И.Левенштейна [3], Э.Одлыжко и Н.Слоэна [4], В.И.Левенштейна [5], [6] с использованием идеи Дельсарта. Изложим эту схему оценки сверху подробно (см. [3], [8, гл.9]). Пусть $\alpha=\frac{m-3}{2} и R_k=R_k^{\alpha,\alpha}, \ k=0,1,2,\ldots,$ есть система ультрасферических многочленов, ортогональных на отрезке $[-1,1]$ с весом $(1-t^2)^\alpha,$ нормированных условием $R_k(1)=1, \ k=0,1,2,\ldots;$ в частности, имеем $R_0(t)=1, R_1(t)=t.$ Обозначим через ${\cal F}={\cal F}_m={\cal F}(\alpha)$ множество непрерывных на отрезке $[-1,1]$ функций $f$ со свойствами:

1) функция $f$ представляется в виде ряда

$$f(t)=\sum_{k=0}^\infty f_k R_k(t),$$ (0.3)

коэффициенты $\{f_k\}^\infty _{k=0}$ которого удовлетворяют условиям:

$$f_0>0, \quad f_k\ge 0, k=1,2,\ldots,$$ (0.4)

$$f(1)=\sum_{k=0}^\infty f_k<\infty;$$ (0.5)

2) функция $f$ - неположительная на отрезке $[-1,\frac{1}{2}]:$

$$f(t)\le 0, -1\le t\le\frac{1}{2}.$$ (0.6)

Известно [3], что множество ${\cal F}_m$ при каждом $m\ge 2$ непусто. На этом множестве функций определим величину

$$w_m=w(\alpha)=\inf\left\{\frac{f(1)}{f_0}: f\in{\cal F}_m\right\}.$$ (0.7)

Обсуждаемая здесь оценка сверху контактного числа $\tau_m$ приведена в следующем утверждении, содержащемся в работах [3], [4], [5], [6] (см. также [8, гл.9, 13 и 14]). Это утверждение приведено здесь с доказательством, поскольку для дальнейшего важным является не только содержащееся в нем неравенство (0.8), но и некоторые моменты из его обоснования.

Теорема A При любом $m\ge 2$ имеет место неравенство

$$\tau _m\le w_m.$$ (0.8)

Доказательство. Важнейшим свойством системы ультрасферических многочленов $R_k=R_k^{\alpha,\alpha}, \alpha=\frac{m-3}{2}, k\ge 0,$ на котором строится доказательство, является свойство положительной определенности (см. [3], [8, гл.9]), состоящее в том, что для произвольного конечного множества $W\subset {\bf S}^{m-1}$ имеет место неравенство

$$\sum_{x,y\in W} R_k(xy)\ge 0,\quad k=0,1,2,\ldots.$$ (0.9)

Это свойство есть следствие следующего соотношения (см. [13, гл.4, §2])

$$R_k(x y) = \frac{\vert{\bf S}^{m-1}\vert}{d_k} \sum_{j=1}^{d_k} \overline{Y_j(x)} Y_j(y),$$

где $\vert{\bf S}^{m-1}\vert$ - площадь сферы ${\bf S}^{m-1}, \ \{Y_1,Y_2,\ldots,Y_{d_k}\}$ - ортонормированный базис в пространстве сферических гармоник степени $k.$ Действительно, из этого соотношения следует, что

$$\begin{eqnarray*} \sum_{x,y\in W} R_k(x y) & = & \sum_{x,y\in W} \frac{\vert{\bf... ...um_{j=1}^{d_k} \left\vert\sum_{x\in W} Y_j(x)\right\vert^2\ge 0. \end{eqnarray*}$$

Свойство (0.9) является нетривиальным лишь при $k\ge 1,$ ибо, поскольку $R_0(t)=1,$ то

$$\sum_{x,y\in W} R_0(x y)=\vert W\vert^2,$$ (0.10)

где $\vert W\vert$ есть мощность множества $W.$

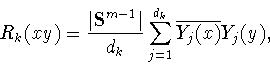
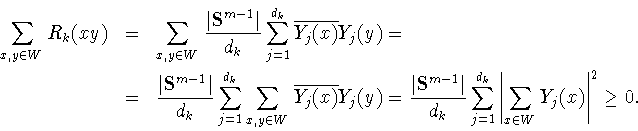
Для произвольного множества $W\subset {\bf S}$ со свойством (0.2) и функции $f\in {\cal F}$ рассмотрим сумму

$$\sum_{x,y\in W} f(x y)=\sum_{x\in W} f(x x) + \sum_{\begin{array}{c} x,y\in W\\ x\ne y \end{array}} f(x y).$$

В правой части этого соотношения первая сумма равна $\vert W\vert f(1)$; вторая же, в силу (0.2) и (0.6), не превосходит нуля. Поэтому справедлива оценка

$$\sum_{x,y\in W} f(x y)\le \vert W\vert f(1).$$

С другой стороны, в силу (0.9), (0.10) и свойства 1) функции $f\in {\cal F}$, имеем

$$\begin{eqnarray*} \sum_{x,y\in W} f(x y) & = & \sum_{x,y\in W} \sum_{k=0}^\infty... ...k=1}^\infty f_k \sum_{x,y\in W} R_k(x y) \ge \vert W\vert^2 f_0. \end{eqnarray*}$$

Сравнивая полученные оценки сверху и снизу суммы $\sum_{x,y\in W} f(x y),$ видим, что справедливо неравенство

$$\vert W\vert\le \frac{f(1)}{f_0}=\frac{\sum_{k=0}^\infty f_k}{f_0}.$$

Отсюда, в силу произвольности множества $W$ со свойством (0.2) и функции $f\in {\cal F},$ следует неравенство

$$\tau_m \le \inf\left \{\frac{f(1)}{f_0}: f\in {\cal F}\right\},$$ (0.11)

которое, очевидно, совпадает с неравенством (0.8). Теорема А доказана.

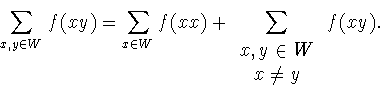
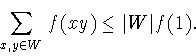
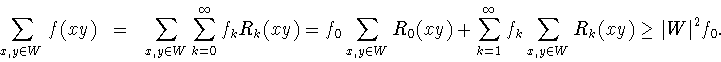
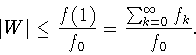
В работах [3], [4], [5], [6] и монографии [8, гл.9, 13 и 14] для оценки сверху контактного числа на самом деле использовалось (содержащееся в (0.8)) неравенство

$$\tau_m \le \frac{f(1)}{f_0}$$ (0.12)

для конкретной функции $f\in {\cal F}.$ Более того, в качестве функции $f$ всегда брался многочлен; есть основания предполагать, что решение задачи (0.7) при любом $m\ge 2$ будет многочленом, т.е. представление (0.3) решения будет содержать лишь конечное число слагаемых. В случае $m=8, 24$ функции (многочлены) $f$ были выбраны так, что неравенство (0.12) дало оценку сверху, совпадающую с известной оценкой снизу. Эта схема, как известно, дает значение $\tau_m$ еще при $m=2.$ Итак, если $m=2, 8, 24,$ то неравенство (0.8) дает точное значение $\tau_m,$ и, кроме того, в этих случаях $\tau_m=w_m.$ К настоящему времени неизвестно, существуют ли еще размерности $m$ с таким свойством или, более обще, с тем свойством, что $\tau_m$ совпадает с целой частью $[w_m]$ числа $w_m.$

В данной работе сделано следующее.

1) Выписана двойственная задача и приведена соответствующая теорема двойственности для задачи несколько более общей, чем (0.7). Как следствие показано, что экстремальная функция задачи (0.7) может иметь лишь конечное число слагаемых с четными номерами.

2) Дано точное решение задачи (0.7) при $m=4.$ При этом оказалось, что $w_4=25.558429097\ldots,$ и решением является многочлен, близкий к выписанному ранее в [4]. Наш результат означает, что неравенство (0.8) не может дать для числа $\tau_4$ оценку сверху, лучшую, чем оценка сверху в (0.1), полученная Э.Одлыжко и Н.Слоэном [4]. Следовательно, для того, чтобы решить вопрос о том, каково же на самом деле значение числа $\tau_4:$ 24 или 25, нужно либо улучшить оценку снизу $\tau_4,$ либо получить принципиально новую оценку сверху.

Переформулируем в удобном для нас виде задачу (0.7). Очевидно, что в (0.7) нижнюю грань достаточно брать на множестве $F=F_m$ функций $f\in{\cal F}_m,$ у которых $f_0=1.$ Поскольку $R_0^{\alpha,\alpha}=1$, то, следовательно, $F$ есть множество функций, представимых в виде

$$f(t)=1+\sum_{k=1}^\infty x_k R_k^{\alpha,\alpha}(t), \quad \alpha=\frac{m-3}{2},$$ (0.13)

где $\{x_k\}_{k=1}^\infty$ есть суммируемая последовательность неотрицательных вещественных чисел, и при этом выполняется свойство (0.6). Полагаем

$$u_m=\inf\left\{\sum_{k=1}^\infty x_k : \ f=1+\sum_{k=1}^\infty x_k R_k^{\alpha,\alpha} \in F_m \right\}.$$ (0.14)

Ясно, что имеет место равенство

$$w_m=1+u_m,$$ (0.15)

и, значит, неравенство (0.8) можно записать в виде

$$\tau_m\le 1+u_m.$$ (0.16)

В следующем пункте будет выписана двойственная задача для задачи несколько более общей, чем (0.14) и приведена соответствующая теорема двойственности.