Пусть ![]() есть (банахово) пространство
непрерывных (вещественных) функций
на отрезке
есть (банахово) пространство
непрерывных (вещественных) функций
на отрезке ![]() с нормой
с нормой
![]() а
а ![]() - (банахово) пространство суммируемых последовательностей
- (банахово) пространство суммируемых последовательностей
![]() вещественных чисел
с нормой
вещественных чисел
с нормой
![]() Пусть
Пусть
![]() есть равномерно ограниченная
последовательность непрерывных функций на
есть равномерно ограниченная
последовательность непрерывных функций на ![]() .
Введем множество
.
Введем множество ![]() последовательностей
последовательностей
![]() с неотрицательными
элементами
с неотрицательными
элементами
![]() таких, что функция
таких, что функция
Обозначим через ![]() конус неотрицательных функций
в пространстве
конус неотрицательных функций
в пространстве ![]() . Относительно функции
. Относительно функции ![]() будем писать, что
будем писать, что
![]() если же
если же
![]() то будем писать, что
то будем писать, что ![]() В
пространстве
В
пространстве ![]() выделим конус
выделим конус ![]() неотрицательных элементов, а точнее, элементов
неотрицательных элементов, а точнее, элементов
![]() удовлетворяющих ограничению
удовлетворяющих ограничению
![]() Условимся писать
Условимся писать
![]() или
или ![]() если соответственно
если соответственно ![]() или
или ![]() Пусть
Пусть ![]() есть линейный оператор, определенный формулой
есть линейный оператор, определенный формулой
Выпишем для ![]() двойственную задачу.
Сопряженное для
двойственную задачу.
Сопряженное для ![]() пространство
пространство ![]() непрерывных линейных функционалов на
непрерывных линейных функционалов на ![]() можно отождествить с пространством
можно отождествить с пространством ![]() функций ограниченной
вариации на
функций ограниченной
вариации на ![]() и при этом непрерывный линейный функционал
на
и при этом непрерывный линейный функционал
на ![]() определяется функцией
определяется функцией ![]() с помощью интеграла
Римана-Стильтьеса по формуле
с помощью интеграла
Римана-Стильтьеса по формуле
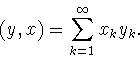
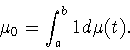
Пусть ![]() есть конус в
есть конус в ![]() , сопряженный конусу
, сопряженный конусу ![]() образованный элементами
образованный элементами
![]() удовлетворяющими условию
удовлетворяющими условию ![]() для любой функции
для любой функции ![]() Нетрудно понять, что
Нетрудно понять, что
![]() состоит из неубывающих на отрезке
состоит из неубывающих на отрезке ![]() функций.
Функцию
функций.
Функцию
![]() мы будем называть
иногда в дальнейшем мерой (на
мы будем называть
иногда в дальнейшем мерой (на ![]() ).
Множество
).
Множество ![]() состоящее из последовательностей
состоящее из последовательностей
![]() с неотрицательными координатами
с неотрицательными координатами ![]() является конусом в
является конусом в ![]() , сопряженным конусу
, сопряженным конусу ![]() Если
Если
![]() или
или
![]() то будем соответственно
писать
то будем соответственно
писать ![]() и
и ![]()
Положим
Исходя из дальнейших применений
взаимосвязи прямой и двойственной задач,
приведем схему возникновения двойственной задачи ![]()
1)
для любой функции
![]() величина
величина
2) для (1.7) имеет место представление
Доказательство.
Для функции ![]() и последовательности
и последовательности ![]() то есть последовательности
то есть последовательности
![]() из конуса
из конуса ![]() для которой функция
для которой функция ![]() определенная формулой (1.1), неположительна на отрезке
определенная формулой (1.1), неположительна на отрезке ![]() будем
иметь следующие соотношения
будем
иметь следующие соотношения
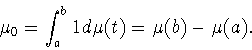
Если
![]() то последнее неравенство
превращается в бессодержательное равенство
то последнее неравенство
превращается в бессодержательное равенство ![]() Допустим, что
Допустим, что
![]() и, значит,
и, значит, ![]() Любой элемент
Любой элемент
![]() очевидно, ненулевой, и
потому для него
очевидно, ненулевой, и
потому для него
![]() В силу этого из (1.11)
следует, что
В силу этого из (1.11)
следует, что ![]() Неравенство (1.11) можно переписать теперь
в виде
Неравенство (1.11) можно переписать теперь
в виде
Убедимся, что для величины ![]() имеет место также формула
(1.7).
Действительно, в (1.9), очевидно, можно ограничиться функциями
имеет место также формула
(1.7).
Действительно, в (1.9), очевидно, можно ограничиться функциями
![]() с
с
![]() т.е.
т.е.
![]() Допустим, что функция
Допустим, что функция
![]() такова, что
такова, что ![]() (напомним, что при этом
(напомним, что при этом ![]() ).
Тогда функция
).
Тогда функция
![]() принадлежит множеству
принадлежит множеству ![]() и для нее
и для нее
![]() Поэтому для
Поэтому для ![]() имеет место формула
имеет место формула
Замечание 1.1
Из приведенных только что
рассуждений видно, что если на функции ![]() достигается
верхняя грань в (1.7) или, то же самое, в (1.14) (т.е.
если
достигается
верхняя грань в (1.7) или, то же самое, в (1.14) (т.е.
если ![]() есть решение этих задач), то
есть решение этих задач), то
![]()
Следующее утверждение, как мы увидим, вытекает из общих фактов теории двойственности задач (бесконечномерного) линейного программирования.
1) задачи ![]() и
и ![]() связаны соотношением двойственности
связаны соотношением двойственности
2) каждая из задач ![]() и
и ![]() имеет решение,
т.е. существуют последовательность
имеет решение,
т.е. существуют последовательность ![]() и функция
и функция
![]() на которых в (1.4) и (1.9) достигаются соответственно
нижняя и верхняя грани;
на которых в (1.4) и (1.9) достигаются соответственно
нижняя и верхняя грани;
3) последовательность
![]() и
функция
и
функция ![]() являются решениями соответственно задач (1.4) и (1.9)
в том и только том случае, если они обладают следующими свойствами:
являются решениями соответственно задач (1.4) и (1.9)
в том и только том случае, если они обладают следующими свойствами:
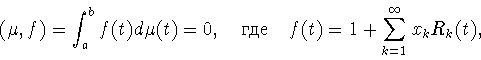
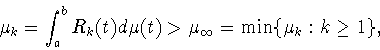
Доказательство теоремы будет проведено с использованием
результатов, приведенных во второй и третьей главах
монографии [14], причем формально эти результаты
следует применять не к задачам ![]() а
к эквивалентным им задачам
а
к эквивалентным им задачам
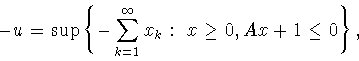
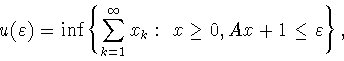
Пространство ![]() является сопряженным для банахова пространства
является сопряженным для банахова пространства ![]() сходящихся к нулю последовательностей
сходящихся к нулю последовательностей
![]() вещественных
чисел с нормой
вещественных
чисел с нормой
![]() Конус
Конус ![]() является
слабо
является
слабо![]() замкнутым множеством (т.е. замкнутым в топологии
замкнутым множеством (т.е. замкнутым в топологии ![]() в стандартных обозначениях [15] и [16])
в пространстве
в стандартных обозначениях [15] и [16])
в пространстве ![]() К задаче
К задаче ![]() применима лемма 1.3 главы 3 из [14].
В силу этой леммы задача (1.4) имеет решение
применима лемма 1.3 главы 3 из [14].
В силу этой леммы задача (1.4) имеет решение ![]()
Допустим, что элемент
![]() принадлежит множеству
принадлежит множеству ![]() т.е. удовлетворяет ограничениям задачи (1.4). При любом
т.е. удовлетворяет ограничениям задачи (1.4). При любом ![]() имеем
имеем
![\begin{displaymath}
1+\sum_{k=1}^\infty \varepsilon x_k R_k(t) \le 1-\varepsilon,\quad
t\in[a,b].
\end{displaymath}](img221.gif)
Пусть элементы ![]() и
и
![]() являются
решениями задач (1.4) и (1.9) соответственно. На этих элементах
неравенство (1.13) обращается в равенство. Из
доказательства (1.13) легко
сделать вывод, что эти
являются
решениями задач (1.4) и (1.9) соответственно. На этих элементах
неравенство (1.13) обращается в равенство. Из
доказательства (1.13) легко
сделать вывод, что эти ![]() и
и ![]() обладают свойствами, указанными в третьем
утверждении теоремы. В частности, найдется номер
обладают свойствами, указанными в третьем
утверждении теоремы. В частности, найдется номер ![]() на котором
достигается минимум:
на котором
достигается минимум:
![]() Обратно, если пара
Обратно, если пара ![]() и
и
![]() обладает указанными в теореме свойствами, то на ней
неравенство (1.13) обращается в равенство. В этом случае имеем
обладает указанными в теореме свойствами, то на ней
неравенство (1.13) обращается в равенство. В этом случае имеем
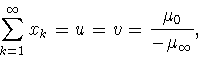
Меру
![]() являющуюся решением двойственной задачи
являющуюся решением двойственной задачи
![]() и одновременно функцию
и одновременно функцию
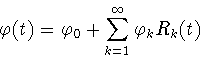
I. Если мера
![]() является решением задачи (1.9),
то на множестве функций
является решением задачи (1.9),
то на множестве функций
![]() имеет место формула
имеет место формула
II. Обратно, если
мера
![]() такова, что на классе
функций
такова, что на классе
функций
![]() имеет
место формула (1.17)
с неотрицательными коэффициентами
имеет
место формула (1.17)
с неотрицательными коэффициентами
![]() и, кроме того,
существует функция
и, кроме того,
существует функция ![]() разложение
(1.16) которой обладает свойствами
(1.19) - (1.20), то
разложение
(1.16) которой обладает свойствами
(1.19) - (1.20), то
![]() мера
мера ![]() является решением двойственной задачи (1.9),
является решением двойственной задачи (1.9),
![]() для коэффициентов
для коэффициентов
![]() формулы (1.17) выполняются соотношения (1.18),
формулы (1.17) выполняются соотношения (1.18),
3) функция ![]() является решением прямой задачи (1.2).
является решением прямой задачи (1.2).
Доказательство. Для любой пары функций
![]() имеем
имеем
Докажем обратное утверждение. Итак, допустим, что для функций
![]() имеет место формула (1.17)
с неотрицательными коэффициентами. Если
имеет место формула (1.17)
с неотрицательными коэффициентами. Если
![]() то
в формуле (1.17)
то
в формуле (1.17)

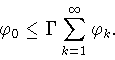
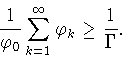
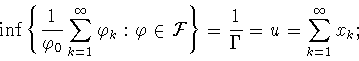
Если последовательность функций ![]() равномерно сходится к нулю на отрезке
равномерно сходится к нулю на отрезке ![]() и число
и число
![]() выбрано так, чтобы при
выбрано так, чтобы при ![]() выполнялось неравенство
выполнялось неравенство
Доказательство.
По предположению функции ![]() равномерно ограничены и всюду
на отрезке
равномерно ограничены и всюду
на отрезке ![]() сходятся к нулю.
Отсюда, в силу теоремы Лебега о мажорантной сходимости (см.,
например, [17, гл.V, §5, п.4]), следует, что
для любой функции
сходятся к нулю.
Отсюда, в силу теоремы Лебега о мажорантной сходимости (см.,
например, [17, гл.V, §5, п.4]), следует, что
для любой функции ![]() и, в частности, для
функции
и, в частности, для
функции ![]() являющейся решением двойственной задачи
(1.9), будет иметь место свойство
являющейся решением двойственной задачи
(1.9), будет иметь место свойство
![]() Поскольку при этом
Поскольку при этом
![]() то существует
лишь конечное число номеров
то существует
лишь конечное число номеров ![]() таких, что
таких, что
![]() В силу третьего утверждения
теоремы 1.1 это влечет первое утверждение следствия.
Далее, для экстремальной меры
В силу третьего утверждения
теоремы 1.1 это влечет первое утверждение следствия.
Далее, для экстремальной меры ![]() при любом
при любом ![]() имеем
имеем
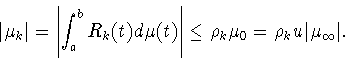
Рассмотрим систему
![]() многочленов Якоби
многочленов Якоби
![]() порядка
порядка ![]() ортогональных на отрезке
ортогональных на отрезке ![]() с весом
с весом
![]() и
нормированных условием
и
нормированных условием ![]() Соответствующая задача (1.2) для системы
Соответствующая задача (1.2) для системы ![]() на отрезке
на отрезке ![]() где
где ![]() изучалась в работах [3],
[6], [7] и в монографии [8, гл.9] в связи
с исследованием верхних границ упаковок компактных римановых симметрических
пространств ранга 1. Так в работе [3] доказано, что если пара
индексов
изучалась в работах [3],
[6], [7] и в монографии [8, гл.9] в связи
с исследованием верхних границ упаковок компактных римановых симметрических
пространств ранга 1. Так в работе [3] доказано, что если пара
индексов
![]() такова, что произведение любых двух многочленов
Якоби представимо в виде линейной комбинации многочленов Якоби с
неотрицательными коэффициентами или, что то же самое,
такова, что произведение любых двух многочленов
Якоби представимо в виде линейной комбинации многочленов Якоби с
неотрицательными коэффициентами или, что то же самое,
Доказательство. Пусть
![]() Обозначим
через
Обозначим
через ![]() функцию, определенную следующим образом
функцию, определенную следующим образом