Rk(t) = 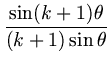 , t = cos , t = cos |
(2.1) |
Для формулировки основного результата работы нам понадобятся несколько
определений и обозначений. Пусть H есть следующий многочлен двадцать
восьмой степени
| H(z) | = | 1744568320000 z28 + 19824640000 z27 - 11368270848000 z26 + | |
| + | 299992125440 z25 + 33683617005056 z24 - 1690611799808 z23 - | ||
| - | 59756580346080 z22 + 3740858012128 z21 + 70524254066704 z20 - | ||
| - | 4516619739088 z19 - 58188563861056 z18 + 3200479271680 z17 + | ||
| + | 34328475907496 z16 - 1262955136312 z15 - 14563330120710 z14 + | ||
| + | 172742066070 z13 + 4417415566665 z12 + 76811504675 z11 - | ||
| - | 942777154875 z10 - 46753060057 z9 + 137285137301 z8 + | ||
| + | 11621133345 z7 - 12856584451 z6 - 1594636173 z5 + | ||
| + | 680106134 z4 + 118057108 z3 - 13255560 z2 - 3691008 z - 186624. | (2.2) |
| z1 | = | -1.0416743109..., z2 = - 0.9918041575..., z3 = - 0.8449780198..., | |
| z4 | = | -0.8175275067..., z5 = - 0.7387597195..., z6 = - 0.5411187835..., | |
| z7 | = | -0.4069720983..., z8 = - 0.2950901339..., z9 = - 0.2696741063..., | |
| z10 | = | -0.1591723800..., z11 = - 0.0913396135..., z12 = 0.4109824855..., | |
| z13 | = | 0.4925150241..., z14 = 0.6197533558..., | (2.3) |
| z15, 16 | = | -0.8891104747...±i 0.1829442719..., | |
| z17, 18 | = | -0.4736286597...±i 0.0577014541..., | |
| z19, 20 | = | 0.4317085516...±i 0.0656750849..., | |
| z21, 22 | = | 0.4484454172...±i 0.0031683147..., | |
| z23, 24 | = | 0.8021254198...±i 0.3917816767..., | |
| z25, 26 | = | 0.9371073469...±i 0.1945583784..., | |
| z27, 28 | = | 1.0751005630...±i 0.2302148263... | (2.4) |
Это утверждение будет получено как следствие приводимой ниже теоремы 2.2.
Введем несколько чисел, выражающихся через d, и функцию,
относительно которой в последствии будет доказано, что она является
экстремальной в задаче w4(d ). Рассмотрим кубический полином
| G | (z) = |
||
| + | 48 d3 - 166 d2 + 16 d + 42 |
(2.7) |
| = | 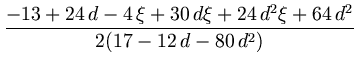 = 0.5035865245..., = 0.5035865245..., |
(2.9) | |
| = | 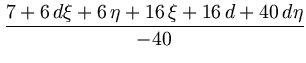 = - 0.0468609188..., = - 0.0468609188..., |
(2.10) | |
| q | = | d + 2 |
(2.11) |
| r | = | 2 d |
(2.12) |
Определим многочлен девятой степени
Ниже мы покажем, что многочлен f* неположителен на отрезке [- 1, d] и коэффициенты Фурье fk* многочлена (2.13) в его разложении по многочленам Чебышева второго рода неотрицательные, причем f*0 > 0, т.е. функция f* принадлежит классу
Доказательство теоремы 2.2 будет реализовано в виде
нескольких вспомогательных утверждений.
Оценку сверху для величины w4(d )
дает функция f*.
Оценка снизу будет
получена с помощью квадратурной формулы (на более широком,
в сравнении с
![]() 4(d ), классе функций),
содержащейся в следующей ниже
лемме 2.1.
4(d ), классе функций),
содержащейся в следующей ниже
лемме 2.1.
Пусть C[- 1, 1] есть пространство вещественных функций непрерывных
на отрезке [- 1, 1]. Обозначим через ![]() множество функций
f
множество функций
f ![]() C[- 1, 1], представимых рядами по многочленам
Rk = Rk1/2, 1/2, k = 0, 1, 2,... с абсолютно суммируемой
последовательностью вещественных коэффициентов:
C[- 1, 1], представимых рядами по многочленам
Rk = Rk1/2, 1/2, k = 0, 1, 2,... с абсолютно суммируемой
последовательностью вещественных коэффициентов:
Многочлен третьей степени
квадрат которого является одним из сомножителей в правой части (2.13), имеет три вещественных корня Эти три числа, обозначения (2.1)-(2.13), (2.16), а также обозначение используются в следующей лемме.
Доказательство. Рассуждения, которые используются для обоснования этой леммы, аналогичны тем, что применялись в работе [8] при доказательстве леммы 4.2, связанной с задачей исследования величины w4 = w4(1/2), поэтому мы приведем эти рассуждения довольно кратко.
Вначале найдем достаточные условия на вещественные узлы
На первом этапе найдем условия, которым должны удовлетворять параметры A, B, C, D. Сделаем симметрическую замену
Рассмотрим многочлен пятой степени
Разложим его вначале по степеням переменной t, а затем, применяя известные (см. [24, с. 28, формула (41) ]) представления степеней переменной через многочлены Чебышева второго рода, найдем нулевой коэффициент, участвующий в разложенииДействуя аналогично, с помощью полинома
и формулы (2.28), находим еще одно выражение для параметра W Приравняв правые части равенств (2.33), (2.35), получим уравнение эквивалентное следующему равенствуТаким же способом, применяя полиномы
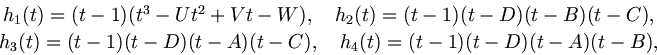 |
(2.37) |
Девять условий (2.33), (2.35), (2.38), (2.39), (2.40), являются необходимыми для существования квадратурной формулы (2.28).
Построим теперь многочлен
![]() (t) =
(t) = ![]()
![]() Rk(t),
на котором зануляются все функционалы, стоящие в правой части
формулы (2.28) (с учетом представления (2.29)), кроме
значения в точке t = 1, т.е. многочлен
Rk(t),
на котором зануляются все функционалы, стоящие в правой части
формулы (2.28) (с учетом представления (2.29)), кроме
значения в точке t = 1, т.е. многочлен ![]() со свойствами
со свойствами
| 10 D + 20 U + 22 W - 32 D2V2U - 32 D2VU + 80 WV - 16 WU2 + | |||
| + | 48 V2U + 32 W2U - 64 D2WU2 + 32 DV3 - 16 D3V2 - 32 D3WU - | ||
| - | 16 D3V + 42 DV + 64 WV2 - 48 VU3 - 64 D3W2 + 64 DWVU - | ||
| - | 24 DU4 - 8 D3U2 - 16 D2U3 + 62 VU + 128 DW2V - 5 D3 - 20 U3 - | ||
| - | 96 WVU2 + DU2 - 128 D2W2U + 128 DW2 - 10 UD2 + | ||
| + | 64 DV2 + 64 DWU - 32 DVU2 - 48 DV2U2 - | ||
| - | 96 DWU3 - 192 DW2U2 |
(2.47) |
Наложим на параметры
D, U, V, W условие: ![]() = 0, т.е.
= 0, т.е.
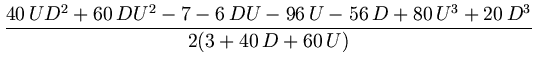 .
.
| F(D, U) = | 4 | +21D + 42U + 320U3D2 + 16DU - 12U2 + 48U3D - 113D3 - | |
| - | 68U3 + 39DU2 + 48UD3 + 160UD4 + 108D2U2 + | ||
| + | 240D3U2 + 12D4 + 80D5 - 166UD2 - 4D2. | (2.49) |
Сейчас мы получим еще одно уравнение относительно неизвестных D, U. Формула (2.28) на функции ![]() (в предположении, что
выполнены условия (2.41)) принимает вид
(в предположении, что
выполнены условия (2.41)) принимает вид
| F1 | (D, U, V, W) = 64 + 122 D + 244 U + 256 V + 422 W + 512 DWV - 672 D2V2U - | ||
| - | 544 D2VU + 1616 WV - 272 WU2 + 816 V2U + 256 DW + 672 W2U - | ||
| - | 1344 D2WU2 + 672 DV3 - 336 D3V2 - 672 D3WU - 272 D3V + 256 DU + | ||
| + | 666 DV + 1344 WV2 - 816 VU3 + 128 U2 - 384 WU3 + 1536 D3W2 + | ||
| + | 1344 DWVU - 128 W2V - 256 D2U2 - 192 V2U2 - 408 DU4 - 136 D3U2 - | ||
| - | 272 D2U3 - 384 U3D - 192 W2U2 - 128 D3W + 910 VU + 3072 DW2V - | ||
| - | 128 D3WV + 256 DWV2 - 256 D2WVU - 384 DWVU2 - 61 D3 - 244 U3 - | ||
| - | 2016 WVU2 + 384 WU + 89 DU2 - 3072 D2W2U - 384 WU2D - 320 V2 - | ||
| - | 256 WUD2 + 3072 DW2 - 128 UD3 + 64 W2 + 512 WUV + 128 V3 - | ||
| - | 512 DVU - 192 U4 - 256 D2VU2 - 384 DVU3 - 128 D3VU + 1008 DV2U2 - | ||
| - | 122 UD2 + 1216 DV2 + 1344 DWU - 544 DVU2 + | ||
| + | 256 V2DU + 2016 DWU3 - 4608 DW2U2. |
| F2(D, U, V) | = | 572 D + 1877 U - 4141 V + 95872 D2V2 + 74240 D2V + 13992 VU2 + | |
| + | 61056 D2V2U + 86592 D2VU - 8192 D4 - 12288 D5 + | ||
| + | 11604 V2U - 30144 DV3 + 258912 D3V2 + 131904 D3V + | ||
| + | 12475 DU - 11352 DV + 1248 VU3 - 36000 D3U3 + 6022 U2 - | ||
| - | 12744 U4D2 - 16640 D4V2 - 27136 D4V - 31080 D2U2 + | ||
| + | 5304 V2U2 - 15216 DU4 - 67472 D3U2 - 54316 D2U3 - | ||
| - | 15960 U3D + 39680 D2V3 - 5184 D3U4 + 8864 VU - 241536 D3U2V - | ||
| - | 153216 D4VU - 59520 U2D2V2 + 20294 D3 + 632 U3 - 69120 D3U3V - | ||
| - | 230400 D3U2V2 + 12566 DU2 - |
||
| - | 22608 U2D4 + 12800 UD3V2 - 38784 UD4 - 46080 U2D4V - | ||
| - | 153600 UD4V2 - 93888 U3D2V - 23040 D5VU - 76800 D5V2 - | ||
| - | 61440 D5V + 153600 D3V3 - 6664 UD3 - 7472 V2 - 3456 U4 - | ||
| - | 86544 D2VU2 - 9216 D5U - 1728 D5U2 + 2160 DVU3 + | ||
| + | 2224 D3VU - 3536 V3 + 25612 UD2 - 37472 DV2 + 39368 DVU2 - | ||
| - | 4160 V2DU + 16896 D2 + 12776 DVU + 45216 DV2U2 |
| = | 68 + 165 D + 42 U - 785 D3 - 1280 D7 - 196 U3 - 640 D2 - 262 D2U - | ||
| - | 4072 D3U2 + 6512 D2U3 - 2280 DU4 + 1528 DU + 1496 D4 + | ||
| + | 1360 D5 + 324 U2 - 816 U4 - 384 D6 + 911 DU2 - 28160 D6U3 - | ||
| - | 58752 D5U3 - 14080 D7U2 - 34944 D6U2 - 15360 D7U - 7168 D6U - | ||
| - | 29376 D4U4 + 10752 D2U4 + 22784 D3U3 + 18960 D3U4 + | ||
| + | 12352 D4U2 - 12256 D4U3 + 20928 D5U + 2576 D5U2 - | ||
| - | 42240 D5U4 - 1192 D2U2 + 3008 D4U - 10216 D3U - 2432 U3D. | (2.52) |
Результант полиномов
F, ![]() по переменой U (см. (2.49),
(2.52))
имеет вид
по переменой U (см. (2.49),
(2.52))
имеет вид
По построению результант полиномов G и T равен нулю, поэтому у
этих полиномов имеется, по крайней мере, один общий корень. Выше
(см. (2.7), (2.8)) говорилось, что полином G имеет два
комплексных корня
![]() = - 0.2486667705...±i 0.0422341143... и один вещественный корень
= - 0.2486667705...±i 0.0422341143... и один вещественный корень
![]() = - 1.3689346636... Поскольку
= - 1.3689346636... Поскольку
Из формул (2.38), (2.39) вытекает, что коэффициенты
![]() ,
,![]() ,
,![]() ,
,![]() функционала
функционала ![]() (см. (2.29)) совпадают с
коэффициентами (2.22)-(2.25) функционала L,
определенного в (2.21). Следовательно, формула (2.28), с
учетом (2.40), примет вид
(см. (2.29)) совпадают с
коэффициентами (2.22)-(2.25) функционала L,
определенного в (2.21). Следовательно, формула (2.28), с
учетом (2.40), примет вид
На данном этапе рассуждений можно утверждать, что
формула (2.53) выполняется на многочленах, определенных
формулами (2.31), (2.34), (2.37) при выбранных
D, U, V, W, A, B, C, а также на многочленах
R6, R7, R8 и
![]() = f*. Указанные десять многочленов образуют базис во
множестве
= f*. Указанные десять многочленов образуют базис во
множестве
![]() 9 многочленов степени не выше девяти. Поэтому
квадратурная формула (2.53) выполняется для любого многочлена
из
9 многочленов степени не выше девяти. Поэтому
квадратурная формула (2.53) выполняется для любого многочлена
из
![]() 9. Из нее, в частности, следует, что L(1) = 1 и
L(R
9. Из нее, в частности, следует, что L(1) = 1 и
L(R![]() ) = 0 при
) = 0 при
![]() = 1, 2, 3, 4, 5, 9, т.е. имеет место
(2.26).
= 1, 2, 3, 4, 5, 9, т.е. имеет место
(2.26).
Очевидно, формулу (2.53) можно распространить на весь класс
функций ![]() , если записать ее в
форме (2.20)-(2.25). Нам осталось проверить неравенства
(2.27). Для обоснования этих неравенств воспользуемся
следующими двумя свойствами многочленов Чебышева второго рода:
1)
R
, если записать ее в
форме (2.20)-(2.25). Нам осталось проверить неравенства
(2.27). Для обоснования этих неравенств воспользуемся
следующими двумя свойствами многочленов Чебышева второго рода:
1)
R![]() (1) = 1,
(1) = 1,
![]()
![]() 0, 2) многочлены R
0, 2) многочлены R![]() на интервале
(- 1, 1) поточечно стремятся к нулю при
на интервале
(- 1, 1) поточечно стремятся к нулю при
![]()
![]()
![]() . Как
следствие этих свойств имеем
L
. Как
следствие этих свойств имеем
L![]() R
R![]()
![]()
![]() 1/25 > 0 при
1/25 > 0 при
![]()
![]()
![]() ;
в силу чего неравенства (2.27) нужно проверить лишь для конечного числа
индексов
;
в силу чего неравенства (2.27) нужно проверить лишь для конечного числа
индексов ![]() . Подробнее, воспользовавшись формулой (2.1), получим
. Подробнее, воспользовавшись формулой (2.1), получим
| L(R |
+ | 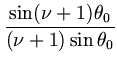 + + 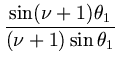 + + |
|
| + | 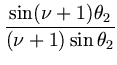 + + 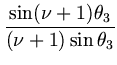 , , |
| = | arccos d = 1.0558191061..., |
||
| = | arccos b = 1.9778305716..., |
| L |
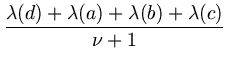 max max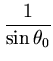 , ,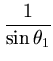 , ,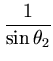 , ,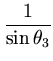 |
||
| = | 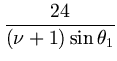 |
В следующей лемме изучаются свойства функция f*, описанной соотношениями (2.5), (2.7)-(2.14).
| f*9 | = | ||
| f*5 | = | ||
| - | |||
| f*4 | = | - |
|
| - | |||
| + | |||
| f*3 | = | ||
| + | rd |
||
| - | |||
| f*2 | = | - |
|
| + | |||
| - | |||
| = | 0.2749299247..., | ||
| f*1 | = | ||
| - | |||
| + | |||
| = | 0.1637887936..., | ||
| f*0 | = | - |
|
| + | |||
| - | |||
| - | (2.54) |
Многочлен f* неположителен на отрезке [- 1, d], ибо последний
множитель
(t2 + qt + r) в его представлении (2.13), имеет
положительный минимум на всей действительной оси:
r - (q/2)2 = 0.248498575...> 0. Кроме того, из формул (2.54), следует, что все
его коэффициенты f*k в разложении (2.14) неотрицательны и
f*0 > 0. Согласно определению (1.4)-(1.6), полином f*
принадлежит множеству
![]() 4(d ).
4(d ).
В силу (2.13), (2.17), (2.18) и (2.54) для функции f* выполняются свойства
Следующая лемма позволит показать, что f* является единственной (c точностью до постоянного положительного множителя) экстремальной функцией задачи w4(d ).
1) для f справедливо представление
где h(t) = (t - d )(t - a)2(t - b)2(t - c)2 =2) в разложении
полинома f по многочленам Чебышева второго рода равны нулю хотя бы два из трех (в частности, все три) коэффициента f6, f7, f8.
Тогда полином f с точностью до постоянного множителя совпадает с
функцией (полиномом) f*, т.е. f = Cf*, где
C = const; при этом, если
f ![]()
![]() 4(d ), то C > 0.
4(d ), то C > 0.
Доказательство леммы проведем в несколько этапов.
1) Допустим вначале, что полином g в представлении (2.55) имеет вид
с некоторыми вещественными коэффициентами Q, R. Выпишем явные выражения коэффициентов f6, f7 и f8 в представлении (2.56) полинома f. Нетрудно убедиться, что гдеНалагая на функцию f любые два из трех условий f6 = 0, f7 = 0,I>f8 = 0, т.е. приравнивая правые части любых двух из трех соотношений (2.59)-(2.61) к нулю, получаем систему
двух линейных уравнений относительно двух неизвестных Q и R. Во всех трех возможных случаях определитель этой системыТаким образом, любая система двух условий (2.62) имеет единственное решение Q, R. В силу (2.13) функция f* имеет представление (2.55) + (2.57) и, согласно (2.54), для нее выполняются условия (2.62). Отсюда следует, что Q = q и R = r. Следовательно, f = f* есть единственная функция, удовлетворяющая условиям (2.55), (2.57) и (2.62).
2) Предположим, что в представлении (2.55) функции f
многочлен g имеет вид
g(t) = Ct2 + Qt + R и при этом C![]() 0. Тогда
функция
fC =
0. Тогда
функция
fC = ![]() удовлетворяет всем условиям
леммы и в ее представлении (2.55) второй множитель имеет вид
(2.57). Отсюда, как мы только что показали, следует, что
удовлетворяет всем условиям
леммы и в ее представлении (2.55) второй множитель имеет вид
(2.57). Отсюда, как мы только что показали, следует, что
![]() = f* или, то же самое, f = Cf*. Ясно,
что если
f
= f* или, то же самое, f = Cf*. Ясно,
что если
f ![]()
![]() 4(d ), то C > 0.
4(d ), то C > 0.
3) Наконец покажем, что если для функции f выполняются условия
леммы, и в соотношении (2.55) второй множитель имеет вид
g(t) = Qt + R, то
f ![]() 0. Действительно, функция
0. Действительно, функция
![]() = f* + f удовлетворяет всем предположениям леммы. Для этой функции
справедлива формула
= f* + f удовлетворяет всем предположениям леммы. Для этой функции
справедлива формула
![]() = h
= h![]() , в которой
, в которой
![]() есть многочлен второй степени
есть многочлен второй степени
![]() (t) = t2 +
(t) = t2 + ![]() t +
t + ![]() с
коэффициентами
с
коэффициентами
![]() = q + Q,
= q + Q, ![]() = r + R. Многочлен
= r + R. Многочлен
![]() имеет вид (2.57). Отсюда, как уже доказано,
следует, что
имеет вид (2.57). Отсюда, как уже доказано,
следует, что
![]() = f*, а потому
f
= f*, а потому
f ![]() 0. Лемма
2.3 доказана полностью.
0. Лемма
2.3 доказана полностью.
Доказательство теоремы 2.2. В силу леммы 2.2
функция f*, определенная соотношением (2.13) принадлежит
множеству
![]() 4(d ) и для нее имеет место равенство
f*(1) = 25f0*. Поэтому справедлива оценка
4(d ) и для нее имеет место равенство
f*(1) = 25f0*. Поэтому справедлива оценка
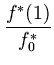 = 25.
= 25.
Докажем обратное неравенство
Для произвольной функции fДля завершения доказательства теоремы 2.2 осталось проверить, что (с точностью до положительного множителя) функция f* является единственной экстремальной. Функция
является экстремальной в том и только в том случае, если на ней неравенство (2.64) обращается в равенство. В силу свойства (2.27) для этого необходимо, чтобы в представлении (2.65) экстремальной функции f коэффициенты f
Доказательство. Рассмотрим многочлен
g(t) = 20t + 1 = 20R1(t) + R0(t). С помощью многочленов f*, g и
числа
![]() , 0
, 0![]()
![]()
![]() 1, определим многочлен
(девятой степени)
1, определим многочлен
(девятой степени)
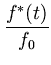 + (1 -
+ (1 -
Полином
F(t) = F(![]() , t) удовлетворяет условию
F(t)
, t) удовлетворяет условию
F(t)![]() 0, - 1
0, - 1![]() t
t![]() s(
s(![]() .) Кроме того, коэффициенты Фурье
Fk, 0
.) Кроме того, коэффициенты Фурье
Fk, 0![]() k
k![]() 9, в разложении F по многочленам Чебышева второго рода,
очевидно, неотрицательные и F0 = 1. Следовательно F принадлежит
классу
9, в разложении F по многочленам Чебышева второго рода,
очевидно, неотрицательные и F0 = 1. Следовательно F принадлежит
классу
![]() 4(s(
4(s(![]() )). Поэтому при
0
)). Поэтому при
0![]()
![]() < 1
имеет место оценка
w4(s(
< 1
имеет место оценка
w4(s(![]() ))
))![]() F(1) = 25
F(1) = 25![]() + (1 -
+ (1 - ![]() )g(1) = 25
)g(1) = 25![]() + (1 -
+ (1 - ![]() )21 < 25 = w4(d ). Отсюда
следует, что
w4(s) < 25 = w4(d ) для
s
)21 < 25 = w4(d ). Отсюда
следует, что
w4(s) < 25 = w4(d ) для
s ![]() [
[![]() , d ). Функция
w4(s) по переменному
s
, d ). Функция
w4(s) по переменному
s ![]() [- 1, 1) не убывает, а потому
w4(s) < 25 = w4(d ) при всех
s
[- 1, 1) не убывает, а потому
w4(s) < 25 = w4(d ) при всех
s ![]() [- 1, d ).
[- 1, d ).
Пусть, теперь, s > d. Нам нужно доказать, что
w4(s) > w4(d )= 25.
Будем рассуждать от противного. Допустим, что
w4(s)![]() w4(d ), а
значит, на самом деле,
w4(s) = w4(d )= 25. В силу теоремы 2.1
работы [8] в задаче w4(s) существует
экстремальная функция; обозначим ее символом fs. Поскольку s > d
и
w4(s) = w4(d ), то функция fs будет являться экстремальной и
в задаче w4(d ). Согласно теореме 2.2 в задаче w4(d )
экстремальная функция единственная (с точностью до положительного
постоянного множителя), и значит, fs = Cf*, C > 0. Однако, если
t
w4(d ), а
значит, на самом деле,
w4(s) = w4(d )= 25. В силу теоремы 2.1
работы [8] в задаче w4(s) существует
экстремальная функция; обозначим ее символом fs. Поскольку s > d
и
w4(s) = w4(d ), то функция fs будет являться экстремальной и
в задаче w4(d ). Согласно теореме 2.2 в задаче w4(d )
экстремальная функция единственная (с точностью до положительного
постоянного множителя), и значит, fs = Cf*, C > 0. Однако, если
t ![]() (d, s], то f*(t) > 0, а
fs(t)
(d, s], то f*(t) > 0, а
fs(t)![]() 0, что противоречиво.
Лемма доказана.
0, что противоречиво.
Лемма доказана.
Доказательство теоремы 2.1. Теорема 2.1 есть следствие теоремы 2.2 и леммы 2.4.