

Next: Bibliography
Up: ab10
Previous: Вычисление значения s4(25).
Определим многочлен
| h(z) |
= |
6068404224 z24 - 5559746560 z23 - 32435331072 z22 + 30162632704 z21 + |
|
| |
+ |
76657888256 z20 - 69950994432 z19 - 105547058176 z18 + 90905438208 z17 + |
|
| |
+ |
93805633312 z16 - 72899067584 z15 - 56276296952 z14 + 37463407248 z13 + |
|
| |
+ |
23144486195 z12 - 12425086062 z11 - 6505367271 z10 + 2613609108 z9 + |
|
| |
+ |
1227229561 z8 - 331172622 z7 - 149222121 z6 + 22205608 z5 + |
|
| |
+ |
10721860 z4 - 490544 z3 - 368104 z2 - 10880 z + 2432. |
(3.1) |
По выше примененной схеме можно доказать следующее утверждение.
Теорема 3.1
На полуинтервале [- 1, 1) уравнение
w4(
s) = 24 имеет единственное
решение:
s =
x12, где
x12 = 0.4785451836... есть двенадцатый
(по возрастанию) вещественный корень полинома (
3.1).
Обоснование этой теоремы базируется на приводимых ниже трех
утверждениях.
В формулировке этих утверждений используются обозначения
d = x12 = 0.4785451836...
есть двенадцатый (по возрастанию) вещественный корень полинома h, заданного
формулой (3.1);
u = - 1.5458619083...
есть единственный вещественный корень многочлена
| G(z) |
= |
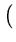 3040 d5 + 2304 d4 - 1264 d3 - 832 d2 + 144 d + 64 3040 d5 + 2304 d4 - 1264 d3 - 832 d2 + 144 d + 64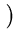 z3 + z3 + |
|
| |
+ |
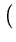 3040 d6 + 2784 d5 - 416 d4 - 720 d3 - 120 d2 + 32 d + 8 3040 d6 + 2784 d5 - 416 d4 - 720 d3 - 120 d2 + 32 d + 8 z2 + z2 + |
|
| |
+ |
 3040 d7 + 2304 d6 - 4184 d5 - 2464 d4 + 1732 d3 + 704 d2 - 204 d - 64 3040 d7 + 2304 d6 - 4184 d5 - 2464 d4 + 1732 d3 + 704 d2 - 204 d - 64 z + z + |
|
| |
+ |
1824 d7 + 288 d6 - 2856 d5 - 753 d4 + 1050 d3 + 255 d2 - 108 d - 24; |
|
v = 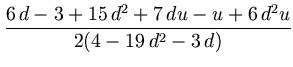 = 0.6856630844... ;
= 0.6856630844... ;
w = 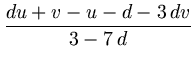 = - 0.082479688... ;
= - 0.082479688... ;
q = 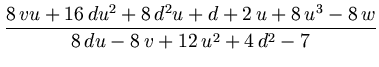 = - 2.1915353439... ;
= - 2.1915353439... ;
| r |
= |
{14 + 30 v + 16 v2 - 16 wu - 13 u2 + 8 duv + 4 u4 + 8 du3 + 12 d2u2 - 8 vd2 - |
|
| |
- |
8 dw + 2 du - 7 d2}/{8 du - 8 v + 12 u2 + 4 d2 - 7} = 1.4453876673... ; |
|
и наконец
a = - 0.8602964888... , b = - 0.4898419662... , c = - 0.1957234532...
есть корни многочлена
z3 - uz2 + vz - w.
Теорема 3.2
Функция
f*(t) = 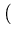 t - d t - d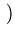 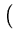 t3 - ut2 + vt - w t3 - ut2 + vt - w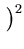 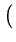 t2 + qt + r t2 + qt + r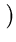
|
(3.2) |
принадлежит множеству
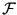 4
4(
d ) и является единственной (с точностью до
положительного постоянного множителя) экстремальной функцией (решением)
задачи (
1.7) при
m = 4,
s =
d; помимо того, справедливы равенства
w4(d )= 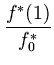 = 24.
= 24.
При доказательстве этой теоремы используются следующие два
утверждения.
Лемма 3.1
Функция
f*, определенная формулой (
3.2), принадлежит
множеству
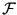 4
4(
d ). Точнее, функция
f* имеет
неотрицательные коэффициенты в ее разложении
f*(
t) =
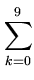 fk*Rk
fk*Rk(
t)
по многочленам Чебышева второго рода, причем,
f*k > 0 при 0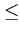 k
k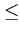 9, k
9, k 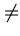 6, 7; f*6 = f*7 = 0.
6, 7; f*6 = f*7 = 0.
Кроме того,
f*(
t)
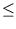
0 при
t 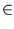
[- 1,
d],
f*(
t) > 0 при
t 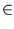
(
d, 1].
Лемма 3.2
Для каждой функции
f (
t) =
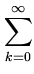 fkRk
fkRk(
t)
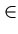
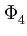
имеет место квадратурная формула
f0 = 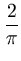
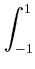 f (t)
f (t)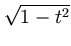 dt = L(f )-
dt = L(f )- 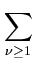 L(R
L(R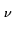 )f
)f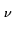 ,
,
в которой
L есть функционал
L(f )= 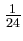 f (1) +
f (1) + 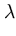 (a)f (a) +
(a)f (a) + 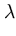 (b)f (b) +
(b)f (b) + 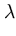 (c)f (c) +
(c)f (c) + 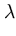 (d )f (d )
(d )f (d )
с коэффициентами
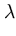 (a) =
(a) = 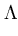 (a, b, c, d )= 0.0996029075... ,
(a, b, c, d )= 0.0996029075... , 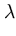 (b) =
(b) = 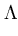 (b, c, d, a) = 0.1465314359... ,
(b, c, d, a) = 0.1465314359... ,
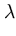 (c) =
(c) = 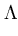 (c, d, a, b) = 0.3337257176... ,
(c, d, a, b) = 0.3337257176... , 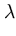 (d )=
(d )= 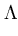 (d, a, b, c) = 0.3784732721... ,
(d, a, b, c) = 0.3784732721... ,
где функция
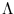
определена формулой (
2.19).
Кроме того, функционал
L обладает свойствами
L(1) = 1; L(R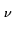 ) = 0 при
) = 0 при 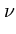 = 1, 2, 3, 4, 5, 8, 9;
= 1, 2, 3, 4, 5, 8, 9;


Next: Bibliography
Up: ab10
Previous: Вычисление значения s4(25).
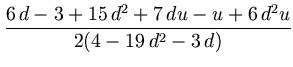 = 0.6856630844... ;
= 0.6856630844... ;
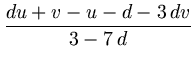 = - 0.082479688... ;
= - 0.082479688... ;
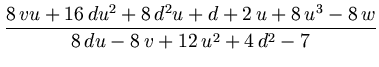 = - 2.1915353439... ;
= - 2.1915353439... ;
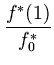 = 24.
= 24.