К задаче (31) приводит также вопрос о точном
неравенстве Джексона - Стечкина в пространстве
![]() вещественных функций на полуоси
вещественных функций на полуоси ![]() со следующим скалярным произведением и нормой
со следующим скалярным произведением и нормой
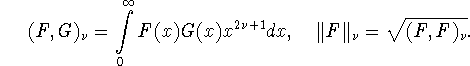
Для функций из ![]() нам понадобятся известные
(см. [28, стр. 112, 113,], комментарии
Н.И.Ахиезера к книге [29], стр. 211, 212, формулы (1), (2))
формулы разложения в интеграл Фурье - Ганкеля по нормированным функциям
Бесселя
нам понадобятся известные
(см. [28, стр. 112, 113,], комментарии
Н.И.Ахиезера к книге [29], стр. 211, 212, формулы (1), (2))
формулы разложения в интеграл Фурье - Ганкеля по нормированным функциям
Бесселя ![]()
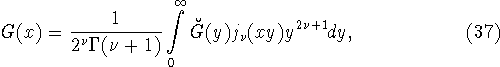
где ![]() есть преобразование Ганкеля функции
есть преобразование Ганкеля функции
![]() т.е.
т.е.
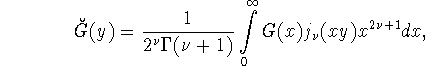
В случае ![]() преобразование Ганкеля
преобразование Ганкеля ![]() переходит в обычное косинус-преобразование Фурье, т.е. для
переходит в обычное косинус-преобразование Фурье, т.е. для ![]() справедливы формулы
справедливы формулы
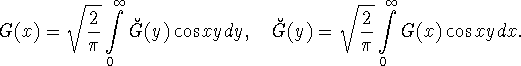
Для ![]() определим класс
определим класс ![]() функций
функций
![]() у которых
преобразование Ганкеля сосредоточено на отрезке
у которых
преобразование Ганкеля сосредоточено на отрезке ![]() т.е.
т.е.
![]()
В пространстве ![]() имеет место следующее равенство Парсеваля
имеет место следующее равенство Парсеваля
![]()
Из этого равенства следует, что для величины
![]()
наилучшего приближения функции ![]() классом
классом ![]() справедлива формула
справедлива формула
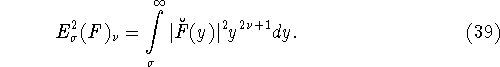
Рассмотрим оператор сдвига ![]() с шагом
с шагом ![]() действующий на функции
действующий на функции ![]() по правилу
по правилу
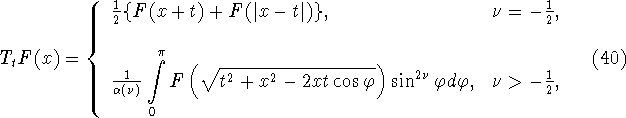
где
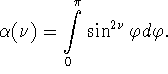 Зафиксируем
Зафиксируем ![]() и рассмотрим действие этого оператора на функцию
и рассмотрим действие этого оператора на функцию
![]() В 1875 году Л.Гегенбауэр
(см. [25, стр. 400,]) доказал важное тождество, именуемое формулой
умножения
В 1875 году Л.Гегенбауэр
(см. [25, стр. 400,]) доказал важное тождество, именуемое формулой
умножения
![]()
т.е.
![]()
В случае ![]() формула (41) переходит в хорошо
известную формулу из тригонометрии
формула (41) переходит в хорошо
известную формулу из тригонометрии
![]()
Свойства оператора сдвига (40) исследовал Б.М.Левитан, который, в частности, доказал [28, стр. 125,] его самосопряженность, при этом существенную роль сыграла формула умножения (41).
Лемма А ([28]).
Для любых функций F, G из пространства ![]() справедливо следующее равенство
справедливо следующее равенство
![]()
Применяя равенства (37), (41), а также соображения п.1 выше,
определим оператор конечной разности порядка r>0 с шагом ![]()
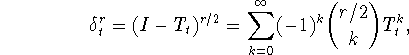
где I - тождественный оператор и ![]() . Соответствующий модуль
непрерывности порядка r>0 функции
. Соответствующий модуль
непрерывности порядка r>0 функции ![]() есть
есть
![]()
Применяя формулу умножения (41) и равенство Парсеваля (38)
для преобразования Ганкеля, приходим к соотношению
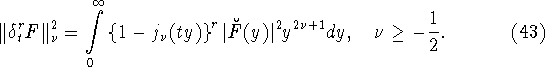
Отсюда и соотношения (39) видно, что при
![]() величина
величина
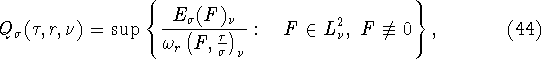
являющаяся точной константой в неравенстве Джексона - Стечкина в
пространстве ![]()
![]()
удовлетворяет равенству
![]()
Следовательно (см. (32)), при
![]() имеем
имеем
![]()