4. Основные результаты.

Напомним, что через мы обозначали первый положительный нуль функции Бесселя индекса (или, что тоже самое, минимальный положительный нуль нормированной функции Бесселя индекса ).

Терема 1.

Пусть Тогда имеют место следующие утверждения

(А)

для каждой ненулевой функции выполняются неравенства

(В)

при существует последовательность функций из такая, что

З а м е ч а н и е 1. Утверждение (В) теоремы 1 является простым следствием довольно общего результата В.В.Арестова [24, п. 3,], [9, лемма 4.2,] и свойств (21), (22).

З а м е ч а н и е 2. Как уже отмечалось выше, при неравенство (48) следует из результата, полученного в совместной работе И.И.Ибрагимова и Ф.Г.Насибова [22], кроме того, при В.Ю.Попов [23] независимо установил результат, из которого следует неравенство (48) и его точность. При неравенство (48) следует из результата В.В.Шалаева [30]. В случае , неравенства (48), (49) следуют из результатов, полученных В.Ю.Поповым [13], [15].

Следствие 1.

Если , то для точной константы  в неравенстве Джексона - Стечкина  в пространстве справедливы соотношения

при

при

Д о к а з а т е л ь с т в о. Равенство (50) вытекает из неравенств (48) и (49) теоремы 1. В силу соотношений (35), (46) неравенство (51) достаточно доказать при т.е. доказать, что при Это неравенство можно получить, например, с помощью функции у которой преобразование Ганкеля имеет вид

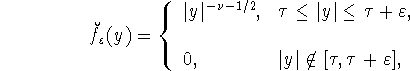
где Действительно, с помощью формул (44), (39) и (43) будем иметь

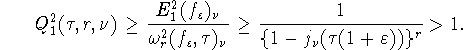
Следствие 1 доказано.

Из равенств (32), (46), теоремы 1 и следствия 1 получаем аналогичные утверждения для задачи (6) о точной константе в неравенстве (5) Джексона - Стечкина в пространстве

Терема 2.

Если то выполняются следующие утверждения

(А)

для любой ненулевой функции справедливы неравенства

(В)

при существует последовательность функций из такая, что

(С)

если то существует функция для которой выполняется строгое неравенство

Следствие 2. Если то величина , определенная равенством , удовлетворяет соотношениям

при

при

при

при

З а м е ч а н и е 3. Неравенство (54) легко получается с помощью функции указанной В.Ю.Поповым в [13, стр. 74,], преобразование Фурье которой имеет вид

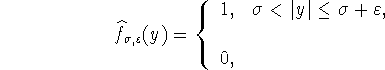
в остальных случаях,

где - достаточно малое положительное число.

З а м е ч а н и е 4. Наряду с замечаниями 1, 2, 3 здесь следует отметить результат В.А.Юдина [10], из которого с помощью рассуждений, содержащихся в работах [13], [14], [15], можно вывести (путем перехода к радиальным функциям и с помощью метода усреднения) равенство (53) при

З а м е ч а н и е 5. Для доказательства утверждения (А) теоремы 1 (при целых и полуцелых ) применялись веса, содержащиеся в работах Н.И.Черныха [7] (случай ), В.Ю.Попова [13] (случай ), В.А.Юдина [10] (случай ).