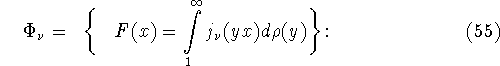
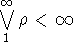 ,
которое является выпуклым подмножеством пространства
,
которое является выпуклым подмножеством пространства
Пусть ![]() Рассмотрим следующее множество функций
Рассмотрим следующее множество функций
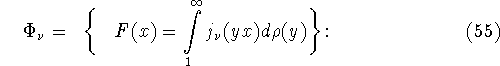
![]() - неубывающая на
- неубывающая на ![]() функция ограниченной вариации
функция ограниченной вариации
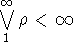 ,
которое является выпуклым подмножеством пространства
,
которое является выпуклым подмножеством пространства ![]()
О п р е д е л е н и е.
Положительное число ![]() назовем точкой Черныха для множества
назовем точкой Черныха для множества ![]() если одновременно выполняются следующие два условия:
если одновременно выполняются следующие два условия:
(a) для любой функции ![]() найдется точка
найдется точка ![]() в
которой
в
которой ![]()
(b) для произвольного числа ![]() найдутся функция
найдутся функция
![]() и число
и число ![]() такие, что
такие, что
![]() при всех
при всех ![]()
Результаты (11), (13) эквивалентны равенству
![]()
Из результатов В.Ю.Попова [13, теорема 3,] следуют неравенства
![]()
Основным результатом этого пункта является
Лемма 1.
Для точки Черныха имеют место следующие двусторонние оценки
![]()
где ![]() - первый положительный нуль нормированной функции Бесселя
- первый положительный нуль нормированной функции Бесселя
![]() индекса
индекса ![]() определенной с помощью
формул
определенной с помощью
формул ![]() и
и ![]() .
.
З а м е ч а н и е 6.
При ![]() в силу равенства (56), имеем
в силу равенства (56), имеем
![]() При
При ![]() оценка сверху
в (58) совпадает с оценкой сверху в (57), а при
оценка сверху
в (58) совпадает с оценкой сверху в (57), а при
![]() уточняет ее, т.к.
уточняет ее, т.к. ![]() (см. [25, гл. 15,]).
(см. [25, гл. 15,]).
Д о к а з а т е л ь с т в ол е м м ы 1.
Оценка снизу ![]() получается с помощью функции
получается с помощью функции
![]() которая, как нетрудно видеть, принадлежит множеству
которая, как нетрудно видеть, принадлежит множеству ![]() Доказательство оценки сверху
Доказательство оценки сверху
![]()
будем проводить по схеме Н.И.Черныха [7]. Построим вес -
неотрицательную, ненулевую и интегрируемую функцию ![]() удовлетворяющую условиям
удовлетворяющую условиям
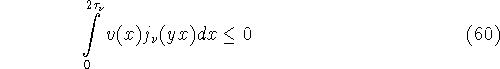
при ![]()
Эти условия будут влечь неравенство (59), т.к. для каждой функции
![]()
где функция ![]() не убывает на полуоси
не убывает на полуоси ![]() и
и
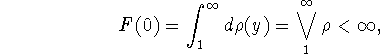
из ![]() будут справедливы соотношения
будут справедливы соотношения
![]()
![]()
Искомый вес при ![]() построил Н.И.Черных [7],
при
построил Н.И.Черных [7],
при ![]() - В.Ю.Попов [13],
а при
- В.Ю.Попов [13],
а при ![]() искомый (одномерный) вес выводится (путем перехода к радиальным функциям)
из (многомерного) веса, который построил В.А.Юдин в работе [10].
"Интерполяция" указанных весов на случай любого (вещественного)
искомый (одномерный) вес выводится (путем перехода к радиальным функциям)
из (многомерного) веса, который построил В.А.Юдин в работе [10].
"Интерполяция" указанных весов на случай любого (вещественного)
![]() приводит к следующей конструкции нужного нам
(одномерного) веса. Положим
приводит к следующей конструкции нужного нам
(одномерного) веса. Положим
![]()
где
![]()
![]() есть оператор сдвига с шагом t (см. (40)).
Нам понадобятся следующие свойства этого оператора [28, § 7,]:
есть оператор сдвига с шагом t (см. (40)).
Нам понадобятся следующие свойства этого оператора [28, § 7,]:
1) если функция ![]() при
при ![]() ,
то
,
то ![]() при
при ![]() ,
,
2) если F(x)=0 при ![]() то
то ![]() при
при ![]()
Из этих свойств вытекает, что вес v, определенный
формулой (61) является неотрицательным и
v(x)=0 для ![]() Поэтому, учитывая самосопряженность сдвига (лемма A) и формулу умножения
Гегенбауэра (41), получаем равенства,
в которых через
Поэтому, учитывая самосопряженность сдвига (лемма A) и формулу умножения
Гегенбауэра (41), получаем равенства,
в которых через ![]() обозначена функция
обозначена функция ![]()
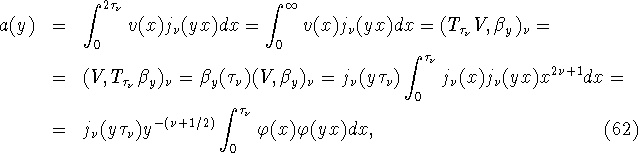
где
![]()
![]() - обычная функция Бесселя индекса
- обычная функция Бесселя индекса ![]() (см. формулу (19)). Как известно
(см. [28, стр. 112,]), функция
(см. формулу (19)). Как известно
(см. [28, стр. 112,]), функция ![]() удовлетворяет следующему
дифференциальному уравнению второго порядка
удовлетворяет следующему
дифференциальному уравнению второго порядка
![]()
где
![]() Применяя стандартный прием с
использованием уравнения (63), получаем
Применяя стандартный прием с
использованием уравнения (63), получаем
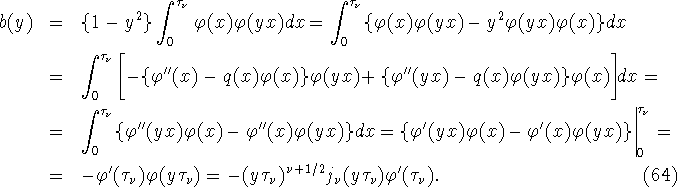
Поскольку
![]()
имеем ![]() Отсюда, (62), (63) и (64) вытекает, что
Отсюда, (62), (63) и (64) вытекает, что
![]()
при ![]() То есть вес v, задаваемый формулой (61), удовлетворяет
условию (60). Лемма доказана.
То есть вес v, задаваемый формулой (61), удовлетворяет
условию (60). Лемма доказана.