


Next: 3.
Up: О схеме Дельсарта оценки
Previous: 1.
Задача (0.14) есть частный случай задачи (1.4);
двойственной для (0.14) будет являться задача
вычисления величины
![\begin{displaymath}
v_m=\sup \left\{\frac{\mu _0}{-\mu_\infty}: \mu
\in V^+\left[-1,\frac{1}{2}\right], \mu\ne{\rm const}\right\},
\end{displaymath}](img327.gif) |
(2.1) |
где
Как мы уже отмечали выше,
множество 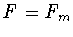 при каждом
при каждом
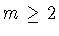 непусто [3]. Поэтому
для задач (0.14) и (2.1) имеет место следующее
утверждение, содержащееся в теореме 1.1.
непусто [3]. Поэтому
для задач (0.14) и (2.1) имеет место следующее
утверждение, содержащееся в теореме 1.1.
Теорема 2.1
При любом
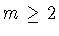
для задач (
0.14) и (
2.1)
справедливы утверждения.
I. Задачи (0.14) и (2.1) связаны
соотношением двойственности
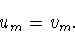 |
(2.2) |
II. Каждая из задач (0.14) и (2.1) имеет решение,
т.е. существуют функция
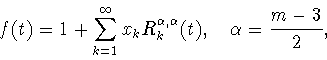 |
(2.3) |
принадлежащая множеству
т.е.
удовлетворяющая ограничениям (
0.4) - (
0.6)),
и функция
![$\mu\in V^+=V^+[-1,\frac{1}{2}],
\mu\ne{\rm const},$](img330.gif)
на которых в (
0.14) и (
2.1) достигаются соответственно
нижняя и верхняя грани.
III. Функции 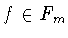 и
и 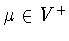 являются решениями соответственно задач (0.14) и (2.1)
в том и только том случае, если они обладают следующими свойствами:
являются решениями соответственно задач (0.14) и (2.1)
в том и только том случае, если они обладают следующими свойствами:
1) определяемая функцией 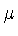 мера сосредоточена на множестве
нулей функции
мера сосредоточена на множестве
нулей функции 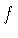 из отрезка
из отрезка
![$[-1,\frac{1}{2}],$](img332.gif)
2) если номер 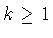 таков, что
таков, что
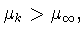 то соответствующий коэффициент
то соответствующий коэффициент 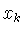 в разложении (2.3) равен нулю:
в разложении (2.3) равен нулю: 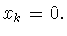
Замечание 2.1
Многочлены
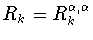 являются четными или нечетными
в соответствии с тем, будет ли число
являются четными или нечетными
в соответствии с тем, будет ли число 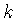 четным или нечетным,
что, в частности, влечет свойство
четным или нечетным,
что, в частности, влечет свойство
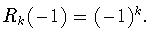 Кроме того, известно (см., например, [20, с.175]), что
Кроме того, известно (см., например, [20, с.175]), что
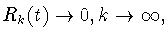 для
для
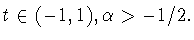 Поэтому, согласно
лемме 1.2, для любой функции
Поэтому, согласно
лемме 1.2, для любой функции
![$\mu \in V[-1,\frac{1}{2}]$](img339.gif) и, в частности, для экстремальной функции
и, в частности, для экстремальной функции 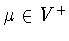 имеем
имеем
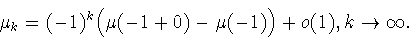 |
(2.4) |
Далее, согласно лемме 1.1, справедливо свойство 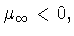 и, значит, равенство
и, значит, равенство
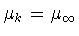 может выполняться лишь
для конечного числа четных номеров
может выполняться лишь
для конечного числа четных номеров 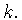 Отсюда, в силу третьего утверждения теоремы 2.1,
следует, что при любом
Отсюда, в силу третьего утверждения теоремы 2.1,
следует, что при любом 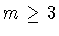 экстремальная функция (2.3)
задачи (0.14) может иметь лишь конечное число ненулевых слагаемых
с четными номерами
экстремальная функция (2.3)
задачи (0.14) может иметь лишь конечное число ненулевых слагаемых
с четными номерами 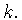 В связи с этим полезно отметить, что
любая функция
В связи с этим полезно отметить, что
любая функция 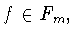 а значит, и экстремальная функция (2.3)
задачи (0.14) обязательно имеет ненулевые слагаемые как с
нечетными,
так и с четными номерами
а значит, и экстремальная функция (2.3)
задачи (0.14) обязательно имеет ненулевые слагаемые как с
нечетными,
так и с четными номерами 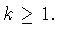 Действительно, функция
Действительно, функция 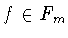 не может быть четной, ибо у нее
не может быть четной, ибо у нее
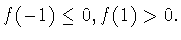 Точно так же,
функция
Точно так же,
функция 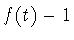 не может быть нечетной, ибо в этом случае
не может быть нечетной, ибо в этом случае 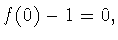 и, как следствие,
и, как следствие, 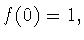 что противоречит предположению
что противоречит предположению 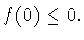



Next: 3.
Up: О схеме Дельсарта оценки
Previous: 1.
![\begin{displaymath}
v_m=\sup \left\{\frac{\mu _0}{-\mu_\infty}: \mu
\in V^+\left[-1,\frac{1}{2}\right], \mu\ne{\rm const}\right\},
\end{displaymath}](img327.gif)
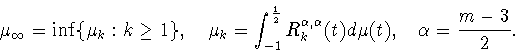
![]() и
и ![]() являются решениями соответственно задач (0.14) и (2.1)
в том и только том случае, если они обладают следующими свойствами:
являются решениями соответственно задач (0.14) и (2.1)
в том и только том случае, если они обладают следующими свойствами:
![]() мера сосредоточена на множестве
нулей функции
мера сосредоточена на множестве
нулей функции ![]() из отрезка
из отрезка
![]()
![]() таков, что
таков, что
![]() то соответствующий коэффициент
то соответствующий коэффициент ![]() в разложении (2.3) равен нулю:
в разложении (2.3) равен нулю: ![]()
![]() являются четными или нечетными
в соответствии с тем, будет ли число
являются четными или нечетными
в соответствии с тем, будет ли число ![]() четным или нечетным,
что, в частности, влечет свойство
четным или нечетным,
что, в частности, влечет свойство
![]() Кроме того, известно (см., например, [20, с.175]), что
Кроме того, известно (см., например, [20, с.175]), что
![]() для
для
![]() Поэтому, согласно
лемме 1.2, для любой функции
Поэтому, согласно
лемме 1.2, для любой функции
![]() и, в частности, для экстремальной функции
и, в частности, для экстремальной функции ![]() имеем
имеем