


Next: 2. Основные результаты.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
Previous: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
Пусть
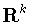 есть
есть  -мерное (
-мерное (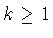 )
вещественное евклидово пространство со скалярным произведением
)
вещественное евклидово пространство со скалярным произведением
 и расстоянием
и расстоянием
 , определенными для
точек
, определенными для
точек
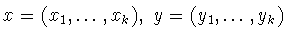 из
из
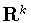 . Обозначим через
. Обозначим через
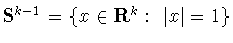 единичную сферу пространства
единичную сферу пространства 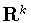 с центром в нуле,
а через
с центром в нуле,
а через
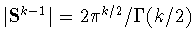 - ее площадь,
в частности,
- ее площадь,
в частности,
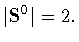
На протяжении всей работы будем считать, что 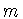 есть
натуральное число не меньше
есть
натуральное число не меньше
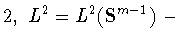 пространство комплексных функций, заданных на
пространство комплексных функций, заданных на 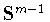 со
скалярным произведением
со
скалярным произведением
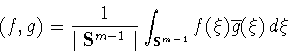 |
(1.1) |
и нормой
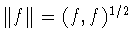 . Многочленом степени не
выше
. Многочленом степени не
выше 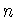 называется функция
называется функция
с комплексными коэффициентами
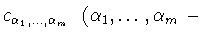 целые неотрицательные числа). Множество сужений
таких многочленов на
целые неотрицательные числа). Множество сужений
таких многочленов на 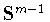 обозначим через
обозначим через
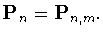 Наилучшим приближением
функции
Наилучшим приближением
функции
 пространством
пространством
 называют
расстояние от
называют
расстояние от 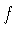 до
до
 , т.е.
, т.е.
Сдвигом с шагом 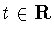 называется (см., например, [19, формулы
(1.1), (1.19)]) оператор
называется (см., например, [19, формулы
(1.1), (1.19)]) оператор 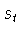 , действующий из
, действующий из 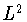 в
в
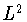 по правилу
по правилу
 |
(1.2) |
здесь
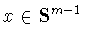 и интеграл берется по сфере
и интеграл берется по сфере
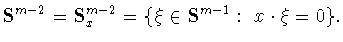 В
частности, при
В
частности, при 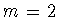 имеем
имеем
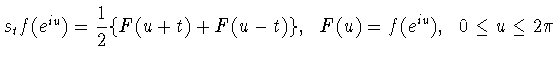 .
.
Пусть 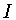 есть тождественный оператор,
есть тождественный оператор, 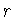 - положительное число,
- положительное число,
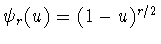 . Следуя Х.П. Рустамову [23],
оператор
. Следуя Х.П. Рустамову [23],
оператор
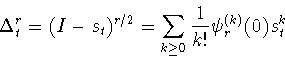 |
(1.3) |
будем называть разностным
оператором порядка 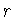 , а модулем непрерывности порядка
, а модулем непрерывности порядка 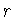 функции
функции
 назовем следующую функцию переменного
назовем следующую функцию переменного 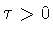
Отметим, что в случае обычного сдвига разностный
оператор дробного порядка был введен и изучался в 1867 - 1868 гг.
А.К.Грюнвальдом и А.В.Летниковым (см. [30, § 20]).
В данной работе изучается вопрос о точной константе
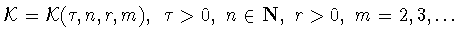 в неравенстве Джексона-Стечкина
в неравенстве Джексона-Стечкина
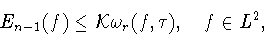 |
(1.4) |
т.е. величина
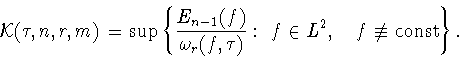 |
(1.5) |
Сферической гармоникой порядка  называют сужение на сферу
называют сужение на сферу
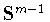 однородного гармонического многочлена степени
однородного гармонического многочлена степени 
Множество всех
гармоник порядка  обозначим символом
обозначим символом 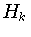 . Известно (см.
[31, гл.4]), что при
. Известно (см.
[31, гл.4]), что при 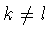 пространства
пространства 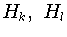 ортогональны в смысле скалярного произведения (1.1), кроме
того, пространство
ортогональны в смысле скалярного произведения (1.1), кроме
того, пространство
 совпадает с ортогональной
прямой суммой
совпадает с ортогональной
прямой суммой
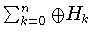 . Справедливо также
разложение пространства
. Справедливо также
разложение пространства 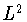 в ортогональную прямую сумму
в ортогональную прямую сумму
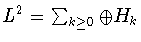 и оператор ортогонального
проектирования
и оператор ортогонального
проектирования
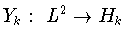 имеет вид (см.
[32, с.206], [31, гл.4,§ 2])
имеет вид (см.
[32, с.206], [31, гл.4,§ 2])
где
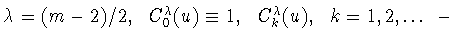 многочлены Гегенбауэра, нормированные условием
многочлены Гегенбауэра, нормированные условием
где
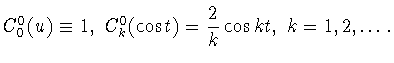 Многочлены
Многочлены
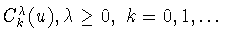 образуют
ортогональную систему на отрезке
образуют
ортогональную систему на отрезке ![$[-1,1]$](img154.gif) с весом
с весом
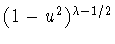 .
.
Каждая функция  единственным образом разлагается в ряд
Фурье-Лапласа, сходящийся к ней в
единственным образом разлагается в ряд
Фурье-Лапласа, сходящийся к ней в 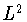
Частичная сумма этого ряда
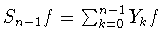 является ближайшим элементом в
является ближайшим элементом в
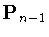 для
для 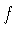 в
метрике пространства
в
метрике пространства 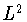 , т.е.
, т.е.
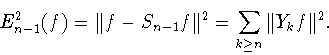 |
(1.6) |
Известны
следующие свойства сдвига 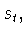 разностного оператора
разностного оператора  и модуля непрерывности
и модуля непрерывности
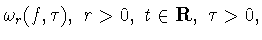 которые выполняются для любой функции
которые выполняются для любой функции 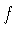 из
из
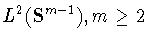
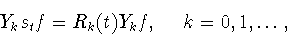 |
(1.7) |
 |
(1.8) |
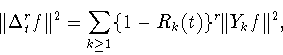 |
(1.9) |
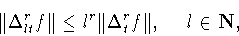 |
(1.10) |
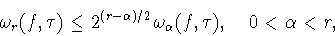 |
(1.11) |
где
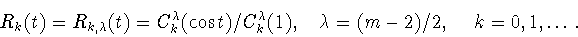 |
(1.12) |
Свойство
(1.10) при 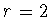 доказал В.А.Иванов [33], в общем
случае оно доказывается так же, остальные свойства можно найти в
работе Х.П.Рустамова [23]. Полиномы (1.12) образуют
ортогональную систему на отрезке
доказал В.А.Иванов [33], в общем
случае оно доказывается так же, остальные свойства можно найти в
работе Х.П.Рустамова [23]. Полиномы (1.12) образуют
ортогональную систему на отрезке ![$[0,\pi]$](img170.gif) с весом
с весом
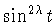
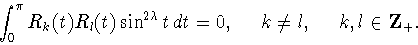 |
(1.13) |
Кроме того, они
удовлетворяют соотношениям
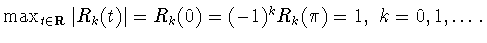
Соотношения (1.6), (1.9) позволяют свести многомерную задачу
(1.5) о точной константе
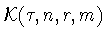 в неравенстве
Джексона-Стечкина (1.4) к одномерной задаче для полиномов (1.12).
А именно, квадрат этой константы совпадает с наименьшей константой
в неравенстве
Джексона-Стечкина (1.4) к одномерной задаче для полиномов (1.12).
А именно, квадрат этой константы совпадает с наименьшей константой
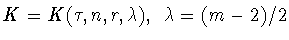 в неравенстве
в неравенстве
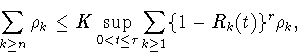 |
(1.14) |
Таким образом,
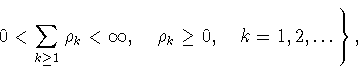 |
(1.15) |
причем для константы (1.5) справедливо равенство
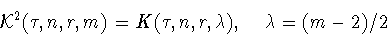 |
(1.16) |
при
 .
.
К задаче (1.15) также сводится (как видно из работ
[34]-[35])
вопрос о точном неравенстве Джексона-Стечкина в пространстве
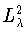 вещественных четных
вещественных четных 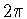 -периодических функций со скалярным
произведением
-периодических функций со скалярным
произведением
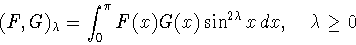 |
(1.17) |
и нормой
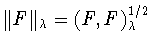 . Как уже
отмечалось выше (см. (1.13)) система (1.12) косинус-полиномов
Гегенбауэра является ортогональной в смысле скалярного
произведения (1.17). Каждая функция
. Как уже
отмечалось выше (см. (1.13)) система (1.12) косинус-полиномов
Гегенбауэра является ортогональной в смысле скалярного
произведения (1.17). Каждая функция 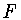 из
из
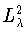 разлагается в ряд Фурье по этим полиномам
разлагается в ряд Фурье по этим полиномам
а частичная сумма этого ряда
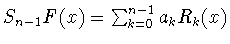 является ближайшей
к
является ближайшей
к 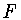 (в смысле нормы
(в смысле нормы
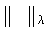 ) косинус-полиномом
порядка
) косинус-полиномом
порядка 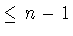 . То есть минимум
. То есть минимум
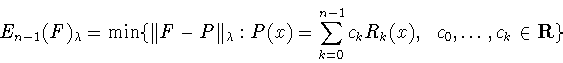 |
(1.18) |
реализует полином 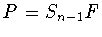
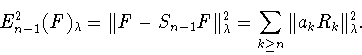 |
(1.19) |
Для функций
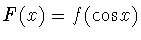 из
из
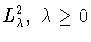 определим
понятие ультрасферического сдвига с шагом
определим
понятие ультрасферического сдвига с шагом 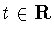 (см.
[34]-[36]), т.е. введем оператор
(см.
[34]-[36]), т.е. введем оператор
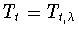 ,
действующий из
,
действующий из
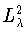 в
в
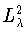 следующим образом
следующим образом
 |
(1.20) |
В 1817 году, а возможно, еще раньше, А.М.Лежандр [37, с.262,
формула (x)], при
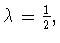 а затем в 1874 году
Л. Гегенбауэр (см. [38, с.402]) при
а затем в 1874 году
Л. Гегенбауэр (см. [38, с.402]) при 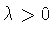 установили
важное свойство этой операции, именуемой формулой умножения,
установили
важное свойство этой операции, именуемой формулой умножения,
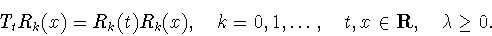 |
(1.21) |
Также как и выше (см.
(1.3)), определим
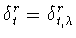 - разностный
оператор порядка
- разностный
оператор порядка 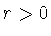 с шагом
с шагом 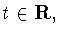 соответствующий сдвигу
соответствующий сдвигу
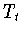 , по формуле
, по формуле
Модулем
непрерывности порядка 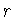 функции
функции 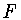 из
из
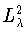 назовем
следующую функцию
назовем
следующую функцию
Из формулы умножения (1.21) вытекают свойства
разностного оператора 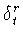 , аналогичные свойствам
(1.8) - (1.11) оператора
, аналогичные свойствам
(1.8) - (1.11) оператора  . В частности, для
каждой функции
. В частности, для
каждой функции
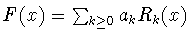 из
из
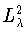 имеем
имеем
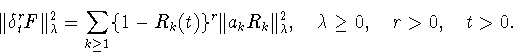 |
(1.22) |
Отсюда и (1.19)
видно, что задача о точной константе
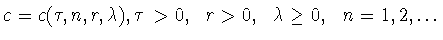 в неравенстве
Джексона-Стечкина
в неравенстве
Джексона-Стечкина
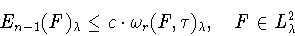 |
(1.23) |
сводится к
задаче (1.15), причем
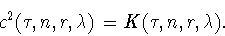 |
(1.24) |
Следовательно (см. (1.16)),
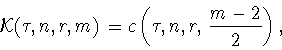 |
(1.25) |
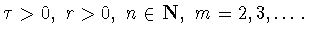 Это
равенство означает, что в (1.5) верхнюю грань достаточно брать
по зональным функциям
Это
равенство означает, что в (1.5) верхнюю грань достаточно брать
по зональным функциям  , т.е. функциям
, т.е. функциям
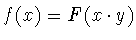 , зависящих лишь от скалярного произведения переменной точки
, зависящих лишь от скалярного произведения переменной точки
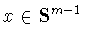 и фиксированной точки
и фиксированной точки
 (см.
[34], [32], [35]).
(см.
[34], [32], [35]).



Next: 2. Основные результаты.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
Previous: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
 , определенными для
точек
, определенными для
точек
![]() есть
натуральное число не меньше
есть
натуральное число не меньше
![]() пространство комплексных функций, заданных на
пространство комплексных функций, заданных на ![]() со
скалярным произведением
со
скалярным произведением
![]() называется (см., например, [19, формулы
(1.1), (1.19)]) оператор
называется (см., например, [19, формулы
(1.1), (1.19)]) оператор ![]() , действующий из
, действующий из ![]() в
в
![]() по правилу
по правилу 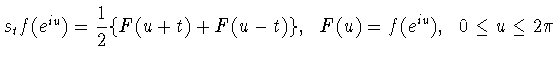 .
.
![]() есть тождественный оператор,
есть тождественный оператор, ![]() - положительное число,
- положительное число,
![]() . Следуя Х.П. Рустамову [23],
оператор
. Следуя Х.П. Рустамову [23],
оператор ![]() в неравенстве Джексона-Стечкина
в неравенстве Джексона-Стечкина
![]() называют сужение на сферу
называют сужение на сферу
![]() однородного гармонического многочлена степени
однородного гармонического многочлена степени ![]()
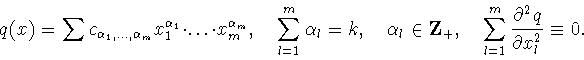
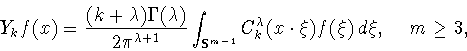
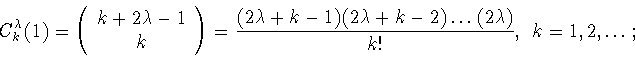
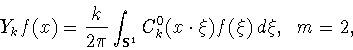
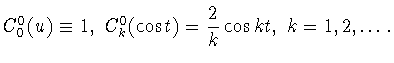 Многочлены
Многочлены
![]() единственным образом разлагается в ряд
Фурье-Лапласа, сходящийся к ней в
единственным образом разлагается в ряд
Фурье-Лапласа, сходящийся к ней в ![]()
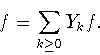
![]() в неравенстве
Джексона-Стечкина (1.4) к одномерной задаче для полиномов (1.12).
А именно, квадрат этой константы совпадает с наименьшей константой
в неравенстве
Джексона-Стечкина (1.4) к одномерной задаче для полиномов (1.12).
А именно, квадрат этой константы совпадает с наименьшей константой
![]() в неравенстве
в неравенстве

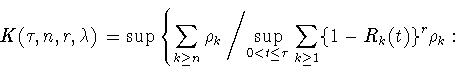
![]() вещественных четных
вещественных четных ![]() -периодических функций со скалярным
произведением
-периодических функций со скалярным
произведением
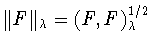 . Как уже
отмечалось выше (см. (1.13)) система (1.12) косинус-полиномов
Гегенбауэра является ортогональной в смысле скалярного
произведения (1.17). Каждая функция
. Как уже
отмечалось выше (см. (1.13)) система (1.12) косинус-полиномов
Гегенбауэра является ортогональной в смысле скалярного
произведения (1.17). Каждая функция 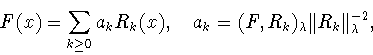
![]() из
из
![]() определим
понятие ультрасферического сдвига с шагом
определим
понятие ультрасферического сдвига с шагом ![]() (см.
[34]-[36]), т.е. введем оператор
(см.
[34]-[36]), т.е. введем оператор
![]() ,
действующий из
,
действующий из
![]() в
в
![]() следующим образом
следующим образом
![]() а затем в 1874 году
Л. Гегенбауэр (см. [38, с.402]) при
а затем в 1874 году
Л. Гегенбауэр (см. [38, с.402]) при ![]() установили
важное свойство этой операции, именуемой формулой умножения,
установили
важное свойство этой операции, именуемой формулой умножения,

