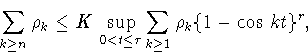
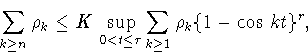

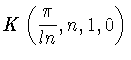 для натуральных
для натуральных
Перейдем к многомерному случаю
![]() . Минимальное положительное значение аргумента функции
. Минимальное положительное значение аргумента функции
![]() , при котором она достигает локального минимума,
локального максимума, обозначим через
, при котором она достигает локального минимума,
локального максимума, обозначим через
![]() и
и
![]() соответственно. Единственный корень уравнения
соответственно. Единственный корень уравнения
![]() обозначим через
обозначим через
![]() . В.Ю. Попов [29] установил, что
. В.Ю. Попов [29] установил, что
Для
![]() обозначим через
обозначим через
![]() первый положительный нуль косинус-полинома Гегенбауэра
первый положительный нуль косинус-полинома Гегенбауэра
![]()
ЗАМЕЧАНИЕ 2.1. Утверждение (B) теоремы 2.1 принадлежит В.В. Арестову (см. ниже лемму 4.2).
ЗАМЕЧАНИЕ 2.2. Для
![]() утверждения
теоремы 2.1 получены Н.И. Черных [6], а при
утверждения
теоремы 2.1 получены Н.И. Черных [6], а при
![]() утверждение (A) теоремы 2.1 доказано В.В.
Шалаевым [39].
утверждение (A) теоремы 2.1 доказано В.В.
Шалаевым [39].
ЗАМЕЧАНИЕ 2.3.
С помощью функции ![]() легко показать, что при
легко показать, что при
![]() точная константа
точная константа
![]() в неравенстве (1.23) будет строго больше единицы.
в неравенстве (1.23) будет строго больше единицы.
В силу равенства (1.25) следствием теоремы 2.1 является
Эта теорема и замечание 2.3 позволяют локализовать точку Черныха в неравенстве Джексона-Стечкина в многомерном случае.
ЗАМЕЧАНИЕ 2.4. Теорема 2.2 для случая ![]() и
и
![]() содержится в работе В.В. Арестова и
В.Ю. Попова [27] (см. (2.4)), а при
содержится в работе В.В. Арестова и
В.Ю. Попова [27] (см. (2.4)), а при
![]() уточняет результат (2.4), т.к.
уточняет результат (2.4), т.к.
![]() (см. [40, с.147, (6.6.4)]).
(см. [40, с.147, (6.6.4)]).
ЗАМЕЧАНИЕ 2.5. В силу известного свойства (1.11) [23, с.130] неравенство (2.9) является следствием неравенства (2.8).
Для доказательства утверждения (A) теоремы 2.1 применялись идеи, заложенные в работах Н.И. Черных [6,7] и В.А. Юдина [24] о построении экстремального веса (решения двойственной задачи).