УДК 517.518.837

ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА
В ПРОСТРАНСТВЕ $\bf L^2$ ФУНКЦИЙ НА МНОГОМЕРНОЙ СФЕРЕ

А. Г. Бабенко

Данная работа посвящена изучению наименьшей константы в неравенстве Джексона-Стечкина для наилучших приближений функций в пространстве $L^2({\bf S}^{m-1})$ на единичной сфере ${\bf S}^{m-1}$ вещественного евклидова пространства ${\bf R}^m$ размерности $m\ge 2$ сужениями на сферу алгебраических многочленов (точнее, сферическими полиномами).

Фундаментальным в этой тематике является результат Д.Джексона для наилучших равномерных приближений непрерывных периодических функций тригонометрическими полиномами. К настоящему времени эта тематика получила большое развитие. Опишем некоторые из известных результатов, имеющих непосредственное отношение к интересам автора.

Обозначим через $C=C_{2\pi}$ пространство вещественных непрерывных $2\pi$-периодических функций $f$ одной вещественной переменной с равномерной нормой $\Vert f\Vert _C=\max\{\vert f(x)\vert\ : x\in{\bf R}\}.$ Наилучшим равномерным приближением функции $f\in C$ тригонометрическими полиномами $t_{n-1}$ степени не выше $n-1$ называется величина

$$E_{n-1}(f)_C=\min_{t_{n-1}}\Vert f-t_{n-1}\Vert _C,$$

а ее равномерным модулем непрерывности порядка $r=1,2,\ldots$ называется функция

$$\omega _r(f,h)_C=\sup_{\vert t\vert\le h}\Vert\sum_{k=0}^r(-1)^k{r\choose k}f(x+kt)\Vert _C$$

переменного $h\ge 0.$ Зафиксируем числа $\tau>0, r\in{\bf N}.$ Хорошо известно следующее неравенство [1], [2], [3]

$$E_{n-1}(f)_C\le{\cal K}\omega_r\left(f,\frac{\tau}{n}\right)_C, \quad n\in{\bf N},\quad f\in C$$ (0.1)

с константой ${\cal K}={\cal K}(\tau,r)<\infty,$ зависящей только от $\tau$ и $r.$ Этот результат означает, что величина

$${\cal K}_n(\tau,r)_C=\sup\left\{\frac{E_{n-1}(f)_C}{\omega _... ...n}\right)_C}:\quad f\in C,\quad f\not\equiv{\rm const}\right\},$$ (0.2)

являющаяся наименьшей константой ${\cal K}$ в неравенстве (0.1) (при фиксированных $\tau, r,n),$ равномерно ограничена по $n,$ т.е. конечна величина

$${\cal K}(\tau,r)_C=\sup_{n\in{\bf N}}{\cal K}_n(\tau,r)_C.$$ (0.3)

Д.Джексон [1] в 1911 году впервые установил неравенство (0.1) при $r=1,$ т.е. оценил наилучшее равномерное приближение $E_{n-1}(f)_{С}$ непрерывной $2\pi$ - периодической функции $f$ тригонометрическими полиномами степени не выше $n-1$ через ее модуль непрерывности $\omega (f,\tau)_C =\omega_1 (f,\tau)_C$ (первого порядка). С.Б.Стечкин [3] получил неравенство (0.1) при $r\ge 2;$ при $r=2$ этот результат был ранее опубликован Н.И. Ахиезером [2, с. 217, с. 190]. Неравенство (0.1) при $r=1$ называют неравенством Джексона, а в общем случае - неравенством Джексона-Стечкина.

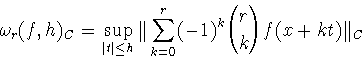
Указанный результат был перенесен на пространства $L^p=L^p_{2\pi}, \ 1\le p<\infty,$ измеримых $2\pi$-периодических функций с обычной нормой (см. [4, гл.5]). Усилиями многих математиков неравенства типа Джексона-Стечкина были распространены на пространства функций многих переменных, заданных как на классических многообразиях (сфера, тор, пространство, гиперболоид, ...), так и на многообразиях довольно общей природы.

Наряду с качественной картиной в этой области большой интерес (в частности, для вычислительных целей) представляют точные результаты. Первое точное неравенство Джексона (в пространстве $C=C_{2\pi})$ установил Н.П.Корнейчук [5] (1962 г.), а первое точное неравенство Джексона-Стечкина (в пространстве $L^2=L^2_{2\pi})$ получил Н.И.Черных [6,7] (1967 г.). Подробнее, Н.П.Корнейчук решил задачу (0.3) при $\tau=\pi, \ r=1,$ доказав равенство ${\cal K}(\pi,1)_C=1.$ Позднее он обобщил этот результат [8] (1982 г.), показав, что ${\cal K}(\pi/m,1)_C=(m+1)/2, \ m\in{\bf N}.$ По аналогии с (0.2) можно дать определение величины ${\cal K}_n(\tau,r)_{L^p},$ являющейся наименьшей константой в соответствующем неравенстве Джексона-Стечкина в пространстве $L^p=L^p_{2\pi}, \ 1\le p<\infty.$ Сейчас наиболее полно изучен случай $p=2.$ Первые точные результаты в этом случае принадлежат Н.И.Черных [6,7], который доказал, что

$${\cal K}_n(\tau,r)_{L^2}=\frac{1}{\sqrt{2r \choose r}}= \fra... ...ad {\mbox при}\quad n,r\in{\bf N},\quad n>r,\quad \tau\ge 2\pi.$$ (0.4)

А в случае $r=1$ им [6,9] была найдена наименьшая точка $\tau^*=\pi,$ начиная с которой величина ${\cal K}_n(\tau,1)_{L^2},$ как функция аргумента $\tau,$ выходит на свой глобальный минимум равный $1/\sqrt 2.$ Точное неравенство Джексона в пространстве $L^p$ при $1\le p<2$ было также установлено Н.И.Черных [10]. В этом случае ${\cal K}_n(\tau,1)_{L^p}$ равна $2^{(1-p)/p}$ при $\tau\ge\theta\pi,$ где $\theta=(1/2-2/\pi^2)^{-1/2}\approx 1.834.$ Как отмечается в работе [10], оценка снизу ${\cal K}_n(\tau,1)_{L^p}\ge 2^{\vert 1/p-1/2\vert-1/2}, \quad 1\le p<\infty,\quad\tau>0,\quad n\in{\bf N}$ была получена ранее В.И.Бердышевым.

Для периодических функций одного вещественного переменного есть еще несколько точных результатов в прямых теоремах теории приближения в терминах модуля непрерывности заданного порядка самой функции. В.В.Жук, В.В.Шалаев получили (см. [11, с.322,352]) соответственно оценки сверху и снизу для величины (0.2) при $r=2, \ \tau=\pi/2,$ с помощью которых вычисляется величина (0.3) в этом случае, а именно, ${\cal K}(\pi/2,2)_C=1.$ В работах автора [12,13] найдены значения величины ${\cal K}_{n}(\pi/m,1)_{L^2}$ для натуральных $m\ge 1+3n/2$ при $n\ge 1$ и для натуральных $m\ge 3n/4$ при $n\ge 10.$ В работе М.Ж.Шакеновой [14] утверждается, что равенство (0.4) остается верным и в случае вещественного $r>0,\ \tau=2\pi.$

Пространства $C_{2\pi}$ и $L^p_{2\pi}$ можно интерпретировать, соответственно, как пространства $C({\bf S}^1), \ L^p({\bf S}^1)$ функций, заданных на единичной окружности ${\bf S}^1$ евклидовой плоскости ${\bf R}^2.$ Одним из естественных обобщений указанных пространств являются пространства $C({\bf S}^{m-1}), \ L^p({\bf S}^{m-1})$ функций, заданных на единичной сфере ${\bf S}^{m-1}$ евклидова пространства ${\bf R}^m$ размерности $m\ge 3$ с центром в нуле.

В 1914 году Т.Гронуол [15] получил неравенство Джексона

$$E_{n}(f)_{C({\bf S}^2)}<(1+3\pi/2)\omega (f,1/n)_{C({\bf S}^2)}, \quad n=2,3,\ldots$$

между наилучшим равномерным приближением функции $f\in C({\bf S}^2), \ f\not\equiv {\rm const},$ сферическими полиномами степени не выше $n$ и ее равномерным модулем непрерывности первого порядка

$$\omega (f,h)_{C({\bf S}^2)}=\sup\{\vert f(x)-f(y)\vert: \ x,y\in{\bf S}^2, \ x\cdot y= \cos t, \ 0<t\le h\},$$ (0.5)

$h\in(0,\pi],$ при условии, что функция $h^{-1}\omega (f,h)_{C({\bf S}^2)}$ не возрастает по $h;$ здесь $x\cdot y$ есть скалярное произведение векторов $x,y.$ В силу известного свойства (см. [16, с.198] и [3, лемма 5])      $2h^{-1}\omega (f,h)_{C({\bf S}^2)}\ge \eta^{-1}\omega (f,\eta)_{C({\bf S}^2)},\quad 0<h<\eta,$ модуля непрерывности произвольной функции $f\in C({\bf S}^2),$ доказательство Т.Гронуола [15, §3] позволяет получить неравенство Джексона

$$E_{n}(f)_{C({\bf S}^2)}<(1+3\pi/\tau)\omega (f,\tau/n)_{C({\bf S}^2)}, \quad 0<\tau/n<\pi,\quad n=2,3,\ldots$$

уже для любой функции $f\in C({\bf S}^2),\ f\not\equiv {\rm const}.$

Дальнейшие исторические сведения, касающиеся неравенств Джексона-Стечкина для функций из $C({\bf S}^{m-1}), \ L^p({\bf S}^{m-1}) , \ m\ge 3$ с применением модулей непрерывности порядка $r\ge 1,$ основанных на $r$-ой разности функции вдоль геодезической, можно найти в работах [17], [18].

Наряду с указанными выше модулями непрерывности многие математики используют другие модули непрерывности, основанные на операторе $s_t$ сдвига, представляющем собой усреднение функции $f(x)$ по границе сферической шапки углового радиуса $t$ c полюсом в точке $x$ (см., например, [19, формулы (1.1), (1.19)], а также пункт 1 ниже, формула (1.2)). Этот оператор сдвига применялся учеными в прошлом веке в вопросах о сходимости ряда Фурье-Лапласа функций, заданных на ${\bf S}^2$ (см., например, [20, с.178 и приведенные там ссылки]). Такой модуль непрерывности для функций $f$ из $C({\bf S}^2)$ в прямых и обратных теоремах теории приближения впервые использовался Г.Г.Кушниренко в работах [21,22]. История дальнейшего развития этого вопроса содержится в работе [23].

Из работ Д.Ньюмена и Г.Шапиро, Д.Рагозина, В.М.Федорова (см. [17] и приведенную там библиографию), относящихся к прямой теореме теории приближения функций на многомерной сфере ${\bf S}^m$ видно, каким образом влияет размерность сферы на указанную теорему. Естественно, что в работы, содержащие соответствующие точные результаты, дают дополнительную информацию о влиянии размерности.

Перечислим несколько точных результатов, относящихся к неравенствам Джексона-Стечкина для функций многих переменных. В 1981 году В.А.Юдин [24] нашел точную константу в неравенстве Джексона для функций из $L^2({\bf T}^m),$ заданных на торе ${\bf T}^m,\ m\ge 2.$ Аналогичная задача в пространстве $L^2({\bf R}^m), \ m=2,3,$ была решена В.Ю. Поповым [25, теорема 3]. В пространстве $C({\bf S}^m), \ m\ge 2$ для наилучших приближений линейными методами В.В.Шалаев [26] получил точный результат в соответствующей прямой теореме теории приближения. В.В.Арестов и В.Ю. Попов [27] указали точное значение наименьшей константы в неравенстве Джексона-Стечкина в пространстве $L^2({\bf S}^m), \ m=2,3.$ В случае пространств $L^2(M), \ M= {\bf R}^m, {\bf T}^m, {\bf S}^m, \ m\ge 2$ В.Ю.Попов [25], [28], [29] нашел точную константу в неравенстве Джексона-Стечкина при "малых" значениях аргумента модуля непрерывности.

В настоящей статье получено точное неравенство Джексона-Стечкина в пространстве $L^2({\bf S}^{m-1}),\ m\geq 5$. Оценка снизу для точной константы в указанном неравенстве установлена В.В. Арестовым и публикуется здесь с доказательством с его разрешения.

Кроме того, в данной работе локализована точка Черныха в этом неравенстве (см.следствие 2.1 ниже), т.е. найдены оценки снизу и сверху (отличающиеся друг от друга в два раза) для наименьшей точки $\tau^*=\tau^*(n,r,m),$ начиная с которой точная константа ${\cal K}={\cal K}(\tau,n,r,m)$ в неравенстве Джексона-Стечкина (см. (1.4), (1.5) ниже) при $r\ge 1$ как функция аргумента $\tau$ выходит на свой минимум (на множестве $\Theta_r),$ равный единице; здесь $\Theta_1=(0,\pi],\ \Theta_r=(0,\pi)$ при $r>1.$ Важность задачи о точке Черныха в неравенстве Джексона-Стечкина состоит, в частности, в том, что она позволяет получить меньшую погрешность при оценке сверху константы в этом неравенстве методом оценки модуля непрерывности в большей точке через значение модуля непрерывности в меньшей точке (см. [8]).