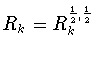 являются многочленами Чебышева второго рода, нормированными условием
являются многочленами Чебышева второго рода, нормированными условием
Ниже в данной работе
будет дано решение задач (0.7),
(0.14) и (2.1) для ![]() При
При ![]() многочлены
многочлены
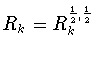 являются многочленами Чебышева второго рода, нормированными условием
являются многочленами Чебышева второго рода, нормированными условием
![]() здесь эти многочлены будут обозначаться символами
здесь эти многочлены будут обозначаться символами ![]() Итак, нас интересует величина
Итак, нас интересует величина
Как уже отмечалось,
![]() Оценка снизу
Оценка снизу ![]() известна давно; эту оценку дают
конкретные классические сферические коды
известна давно; эту оценку дают
конкретные классические сферические коды
![]() которые можно найти, например,
в монографии [8, Т.1, гл.1, §2, п.2.4].
Оценка сверху
которые можно найти, например,
в монографии [8, Т.1, гл.1, §2, п.2.4].
Оценка сверху ![]() была получена Э.Одлыжко и Н.Слоэном
[4] (см. также [8, гл.13])
с помощью неравенства (0.12). Для обоснования этой оценки они
нашли конкретную функцию
была получена Э.Одлыжко и Н.Слоэном
[4] (см. также [8, гл.13])
с помощью неравенства (0.12). Для обоснования этой оценки они
нашли конкретную функцию ![]() а точнее, многочлен девятой степени
а точнее, многочлен девятой степени
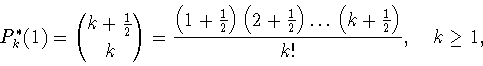
Приведенный только что результат Э.Одлыжко и Н.Слоэна влечет оценку
Точное решение задачи (3.1) было нами получено по следующей схеме.
Вначале мы провели эксперимент на компьютере,
численно решая задачу линейного программирования,
являющуюся дискретизацией задачи (3.1);
дискретизация состояла в том, что бесконечная сумма (3.2)
была заменена на довольно большую конечную (до 40 слагаемых), и
условие неположительности функции ![]() на отрезке
на отрезке
![]() было заменено аналогичным условием на
достаточно густой сетке
из отрезка
было заменено аналогичным условием на
достаточно густой сетке
из отрезка ![]() В результате был получен многочлен
В результате был получен многочлен
1) его коэффициенты ![]() с номерами
с номерами ![]() равны нулю:
равны нулю:
2) многочлен ![]() имеет на отрезке
имеет на отрезке ![]() три двойных корня
три двойных корня ![]() и простой корень
и простой корень
![]()
Допустим теперь, что точное решение ![]() задачи
задачи ![]() имеет указанный здесь вид (3.5) - (3.7).
В силу теоремы 2.1 можно утверждать, что решение
имеет указанный здесь вид (3.5) - (3.7).
В силу теоремы 2.1 можно утверждать, что решение
![]() соответствующей двойственной задачи
(т.е. задачи (2.1) для
соответствующей двойственной задачи
(т.е. задачи (2.1) для ![]() )
есть мера, сосредоточенная в точках
)
есть мера, сосредоточенная в точках ![]() и, значит, на функциях
и, значит, на функциях ![]() имеет место формула
имеет место формула
1) Функция ![]() имеет вид
имеет вид

2) Разложение (3.5) функции ![]() по многочленам Чебышева второго рода
имеет неотрицательные коэффициенты
по многочленам Чебышева второго рода
имеет неотрицательные коэффициенты ![]() и при этом
и при этом
![]()
3) Параметры
![]() меры
меры ![]() таковы,
что коэффициенты
таковы,
что коэффициенты
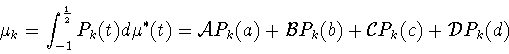
Перечисленные условия дают систему девяти (нелинейных) уравнений
с девятью неизвестными, которыми являются параметры
![]() и два коэффициента
и два коэффициента
![]() многочлена
многочлена
![]() Полученную систему мы успешно решили на компьютере с помощью пакета
аналитических вычислений Maple.
Полученную систему мы успешно решили на компьютере с помощью пакета
аналитических вычислений Maple.
Расчеты на компьютере позволили нам построить функции ![]() и
и ![]() экстремальность же этой пары функций обосновывается ниже аналитически, без
привлечения компьютера.
В приводимых рассуждениях мы выписываем приближенные значения всех
встречающихся переменных (корней уравнений и необходимых функций этих
корней), что позволит читателю, при необходимости, провести нужную
локализацию этих переменных.
экстремальность же этой пары функций обосновывается ниже аналитически, без
привлечения компьютера.
В приводимых рассуждениях мы выписываем приближенные значения всех
встречающихся переменных (корней уравнений и необходимых функций этих
корней), что позволит читателю, при необходимости, провести нужную
локализацию этих переменных.
Численные расчеты на компьютере дискретного аналога задачи (3.1) были осуществлены авторами посредством программы решения задач линейного программирования с малым числом неизвестных и большим числом ограничений, любезно предоставленной нам Л.В.Петрак; при проведении аналитических расчетов на компьютере в пакете Maple большую помощь нам оказали С.В.Бердышев и М.В.Дейкалова. Всем им авторы весьма благодарны.
Для формулировки результатов оставшейся части работы нам
понадобятся несколько определений и обозначений.
Пусть ![]() есть следующий многочлен седьмой степени
есть следующий многочлен седьмой степени

Одним из основных результатов данной работы является следующее утверждение.
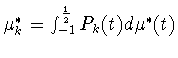 и величина
и величина
Предварительно докажем несколько
вспомогательных утверждений. Ниже будут
использоваться следующие известные
(см., например, [21, с.30]) разложения степеней
переменной через многочлены
Доказательство.
В правой части (3.15) многочлен
![]() положительный на всей вещественной оси, ибо
положительный на всей вещественной оси, ибо
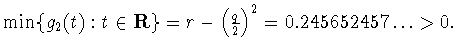 Поэтому
Поэтому
Нам осталось доказать, что в разложении (3.16)
функции (3.15) по многочленам
Чебышева второго рода
коэффициенты ![]() неотрицательные, причем
неотрицательные, причем
![]() Вначале разложим
Вначале разложим ![]() по степеням переменной
по степеням переменной ![]()
Доказанная только что лемма дает оценку сверху величины ![]() и, как мы увидим в дальнейшем, эта оценка точная.
Для обоснования нужной оценки снизу величины
и, как мы увидим в дальнейшем, эта оценка точная.
Для обоснования нужной оценки снизу величины ![]() мы сейчас построим
специальную квадратурную формулу, содержащую не только значения
функции, но и ее коэффициенты Фурье по многочленам Чебышева второго
рода;
по существу эта формула является формулой (1.17) для задач
мы сейчас построим
специальную квадратурную формулу, содержащую не только значения
функции, но и ее коэффициенты Фурье по многочленам Чебышева второго
рода;
по существу эта формула является формулой (1.17) для задач
![]() .
.
Доказательство.
Вначале найдем достаточные условия на вещественные узлы
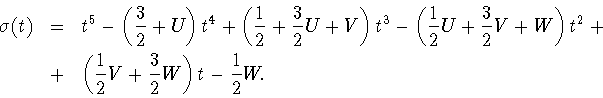
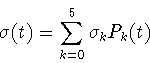
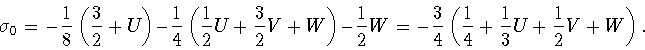
Сейчас мы выразим коэффициенты
![]() квадратурной
формулы (3.42) - (3.43) через
квадратурной
формулы (3.42) - (3.43) через ![]() и
и ![]() Начнем с
Начнем с ![]() Рассмотрим многочлен четвертой степени
Рассмотрим многочлен четвертой степени
Аналогично, используя многочлен
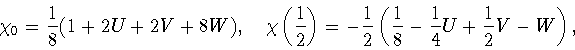
По этой же схеме с помощью многочленов
Подставляя в (3.42) многочлены
![]() получим еще три необходимых условия
получим еще три необходимых условия
Построим теперь многочлен
![]() на котором зануляются все функционалы, стоящие в правой
части формулы (3.42), кроме значения в точке
на котором зануляются все функционалы, стоящие в правой
части формулы (3.42), кроме значения в точке ![]() т.е.
многочлен со свойствами
т.е.
многочлен со свойствами
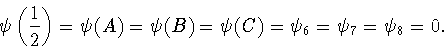
В квадратурной формуле
(3.42) имеется 11 параметров, в то время как любой многочлен девятой
степени определяется с помощью 10 коэффициентов.
В связи с этим мы имеем возможность наложить
на параметры квадратурной формулы условие
Формула (3.42) с дополнительным
условием (3.64) (или, что то же самое, (3.65)) на ее
параметры на многочлене ![]() принимает вид
принимает вид
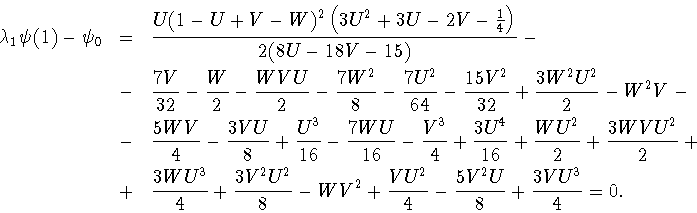
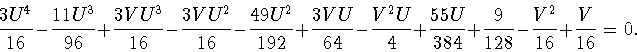
Как уже говорилось выше, многочлен ![]() (а значит, и уравнение
(3.69)) имеет три вещественных корня.
Нас интересует решение, обеспечивающее
выполнение условий (3.41);
этим свойством обладает лишь решение (3.10).
В связи с этим, с данного момента предполaгается, что
(а значит, и уравнение
(3.69)) имеет три вещественных корня.
Нас интересует решение, обеспечивающее
выполнение условий (3.41);
этим свойством обладает лишь решение (3.10).
В связи с этим, с данного момента предполaгается, что ![]() При этом предположении, в силу формул (3.66), (3.48),
(3.57), (3.58),
(3.11) - (3.14) имеем
При этом предположении, в силу формул (3.66), (3.48),
(3.57), (3.58),
(3.11) - (3.14) имеем
![]() Отсюда следует, что
многочлен (3.46) совпадет с многочленом
(3.17), а потому
Отсюда следует, что
многочлен (3.46) совпадет с многочленом
(3.17), а потому
На данном этапе рассуждений можно утверждать, что
формула (3.71)
выполняется на многочленах
(3.47), (3.49), (3.52), (3.54), а
также на многочленах ![]() и
и ![]() Указанные десять многочленов
образуют базис во множестве
Указанные десять многочленов
образуют базис во множестве ![]() многочленов степени
не выше девяти. Поэтому квадратурная формула (3.71)
выполняется для любого многочлена из
многочленов степени
не выше девяти. Поэтому квадратурная формула (3.71)
выполняется для любого многочлена из ![]() Из нее, в частности, следует, что
Из нее, в частности, следует, что ![]() при
при
![]() т.е. имеет место (3.39).
Подставив в формулу
(3.71) многочлен
т.е. имеет место (3.39).
Подставив в формулу
(3.71) многочлен ![]() получаем
также утверждение (3.38).
получаем
также утверждение (3.38).
Очевидно, формулу (3.71)
можно распространить на весь класс
функций ![]() если записать ее в форме (3.31) - (3.37).
Нам осталось проверить неравенства (3.40).
Для обоснования этих неравенств воспользуемся следующими двумя
свойствами многочленов Чебышева второго рода:
1)
если записать ее в форме (3.31) - (3.37).
Нам осталось проверить неравенства (3.40).
Для обоснования этих неравенств воспользуемся следующими двумя
свойствами многочленов Чебышева второго рода:
1)
![]() 2) многочлены
2) многочлены ![]() на интервале
на интервале ![]() поточечно стремятся к нулю
при
поточечно стремятся к нулю
при ![]() Как следствие этих свойств имеем (ср. с леммой 1.2)
Как следствие этих свойств имеем (ср. с леммой 1.2)
![]() в силу чего неравенства (3.40) нужно проверить лишь для конечного
числа индексов
в силу чего неравенства (3.40) нужно проверить лишь для конечного
числа индексов ![]() Подробнее,
воспользовавшись соотношениями (3.24), имеем
Подробнее,
воспользовавшись соотношениями (3.24), имеем
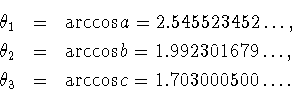

Доказательство теоремы 3.1. Для функции,
а на самом деле, - многочлена девятой степени
![]() определенного соотношением (3.15), выполняются свойства
определенного соотношением (3.15), выполняются свойства


Для произвольной функции
![]() справедлива
квадратурная формула (3.31) - (3.32).
Коэффициенты
справедлива
квадратурная формула (3.31) - (3.32).
Коэффициенты
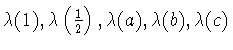 этой формулы положительные,
а коэффициенты
этой формулы положительные,
а коэффициенты
![]() - неотрицательные
(точнее,
- неотрицательные
(точнее,
![]() и
и
![]() ).
В силу свойств (0.3) - (0.6) функции
).
В силу свойств (0.3) - (0.6) функции
![]() отсюда следует оценка
отсюда следует оценка
Пусть ![]() есть мера на
есть мера на
![]() сосредоточенная в точках
сосредоточенная в точках
![]() и
и ![]() с весами (3.34) - (3.37).
Очевидно, справедливо соотношение
с весами (3.34) - (3.37).
Очевидно, справедливо соотношение
![\begin{displaymath}
\int_{-1}^{\frac{1}{2}} f(t)d\mu(t)=
L(f)-\lambda(1)f(1),\quad f\in C[-1,1],
\end{displaymath}](img649.gif)
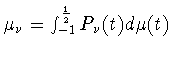 этой меры имеем представление
этой меры имеем представление
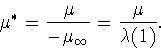
Доказанная только что теорема 3.1 дает точное решение задач
![]() Сейчас мы дадим довольно простую,
в сравнении с точным решением, оценку снизу этих трех
величин.
Сейчас мы дадим довольно простую,
в сравнении с точным решением, оценку снизу этих трех
величин.
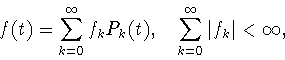
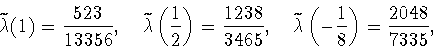
Доказательство.
Формула (3.76), очевидно, выполняется для многочленов
![]() при любом
при любом ![]() Справедливость этой формулы для многочленов
Справедливость этой формулы для многочленов
![]() при
при ![]() нетрудно обосновать непосредственными
вычислениями. Проверка неравенства (3.79) проводится по той же схеме,
как это делалось в лемме 3.2 при доказательстве
неравенств (3.40). Теорема 3.2 доказана.
нетрудно обосновать непосредственными
вычислениями. Проверка неравенства (3.79) проводится по той же схеме,
как это делалось в лемме 3.2 при доказательстве
неравенств (3.40). Теорема 3.2 доказана.
Из формулы (3.76) легко следует (см. доказательство (3.74))
неравенство
![]() и, как следствие, неравенство
и, как следствие, неравенство
![]() Таким образом, теорема 3.2 дает оценку
Таким образом, теорема 3.2 дает оценку
4. Нам приятно выразить нашу признательность В.А.Юдину. Именно в результате неоднократных обсуждений данной тематики с В.А.Юдиным у авторов возник интерес к ней, и, как следствие, - появилась эта работа.
Научное и человеческое общение с С.Б.Стечкиным оказало огромное влияние на нас и наши научные интересы, за что мы всегда будем ему благодарны. Большое место в его научных исследованиях и исследованиях его учеников уделялось экстремальным задачам и, в частности, экстремальным задачам для функций, представимых рядами по различным системам, с ограничениями на значения функций и коэффициенты разложений, каковыми и являются обсуждаемые здесь задачи.