


Next: 4. Вспомогательные утверждения.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
Previous: 2. Основные результаты.
В этом пункте приводятся необходимые в дальнейшем
известные свойства (см. [34,35]) оператора
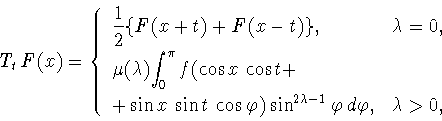 |
(3.1) |
ультрасферического сдвига с шагом 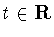 , действующего
на функции
, действующего
на функции 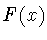 вида
вида
ЛЕММА 3.1
Пусть
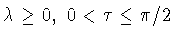
, функция
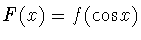
непрерывна при всех
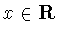
и
Тогда функция
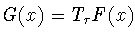
является непрерывной при
всех
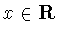
и
ДОКАЗАТЕЛЬСТВО.
При 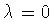 утверждения леммы легко
проверяются. Пусть
утверждения леммы легко
проверяются. Пусть 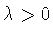 . Непрерывность функции
. Непрерывность функции  очевидна.
По условию леммы имеем
очевидна.
По условию леммы имеем
![\begin{displaymath}
f(u)=0,\ \ \ \ u \in [-1, \cos \tau ].
\end{displaymath}](img289.gif) |
(3.2) |
Функция
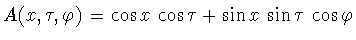 принимает свои значения в отрезке
принимает свои значения в отрезке
![$[-1, \cos \tau ]$](img291.gif) , если
, если
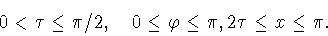 |
(3.3) |
Действительно, в этом случае
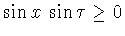 ,
поэтому при фиксированных
,
поэтому при фиксированных
![$\tau \in (0, \pi/2],\ x \in [2\tau, \pi]$](img294.gif) функция
функция
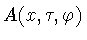 монотонно изменяется в отрезке
монотонно изменяется в отрезке
![$[\cos (x+\tau),\ \cos(x-\tau)]$](img296.gif) , когда
, когда 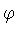 меняется от
меняется от
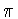 до
до 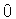 , при этом
, при этом
![$[\cos (x+\tau ),\ \cos(x-\tau)] \subseteq [-1, \cos \tau]$](img300.gif) .
Поэтому
.
Поэтому
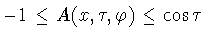 , если выполнено
(3.3). Отсюда, (3.1) и (3.2) получаем утверждение леммы.
, если выполнено
(3.3). Отсюда, (3.1) и (3.2) получаем утверждение леммы.
Напомним, что через
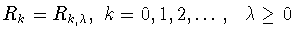 мы обозначали полиномы
мы обозначали полиномы
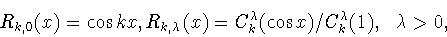 |
(3.4) |
где
есть многочлен Гегенбауэра (ультрасферический многочлен) (см.
[40, стр. 96, формула (4.7.31)]). Известны (см.
[40, с.91,92,175], [38, с.399]) следующие свойства
полиномов (3.4)
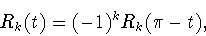 |
(3.5) |
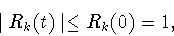 |
(3.6) |
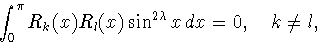 |
(3.7) |
где
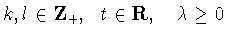 . В частности, в пространстве
. В частности, в пространстве
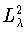 функций со
скалярным произведением
функций со
скалярным произведением
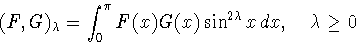 |
(3.8) |
полиномы
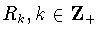 образуют ортогональную систему.
образуют ортогональную систему.
В 1954 году С. Бохнер [34] (см. также [35]) ввел понятие
ультрасферической свертки для функций
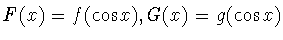 из
из
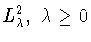
и, опираясь на результат (1.22) Л. Гегенбауэра, доказал
коммутативность этой операции
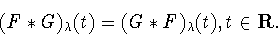 |
(3.9) |
Поскольку
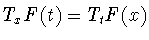 для любых
для любых 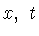 из
из
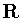 , то равенство (3.9) означает самосопряженность
ультрасферического сдвига. То есть справедлива
, то равенство (3.9) означает самосопряженность
ультрасферического сдвига. То есть справедлива
ЛЕММА 3.2
Пусть
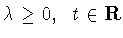
и функции
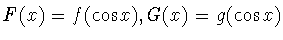
принадлежат пространству
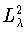
. Тогда справедливо равенство
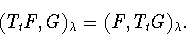 |
(3.10) |



Next: 4. Вспомогательные утверждения.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
Previous: 2. Основные результаты.
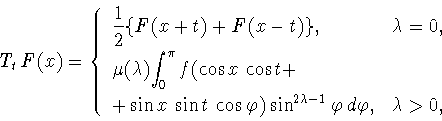
![]() утверждения леммы легко
проверяются. Пусть
утверждения леммы легко
проверяются. Пусть ![]() . Непрерывность функции
. Непрерывность функции ![]() очевидна.
По условию леммы имеем
очевидна.
По условию леммы имеем
![]() мы обозначали полиномы
мы обозначали полиномы ![\begin{displaymath}C^{\lambda }_k (u)=\sum^{[k/2]}_{l=0}\frac{(-1)^l \Gamma (k-l...
...^{k-2l}} {\Gamma (\lambda ) \, \Gamma (l+1) \, \Gamma (k-2l+1)}\end{displaymath}](img304.gif)
![]() из
из
![]()