


Next: 2. Формулировка основного результата.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
В этой работе доказано точное неравенство
Джексона-Стечкина в пространстве 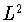 на отрезке с весом Якоби,
и, как следствие, получены родственные неравенства для функций
многих переменных, заданных на проективных пространствах. Указанный
результат для приближений на отрезке, в основном, был анонсирован
ранее автором в [2].
на отрезке с весом Якоби,
и, как следствие, получены родственные неравенства для функций
многих переменных, заданных на проективных пространствах. Указанный
результат для приближений на отрезке, в основном, был анонсирован
ранее автором в [2].
Пусть
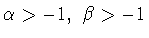 и
и
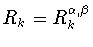 -
алгебраические многочлены Якоби порядка
-
алгебраические многочлены Якоби порядка
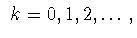 ортогональные на отрезке
ортогональные на отрезке ![$[-1,1]$](img7.gif) c весом
c весом
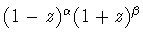 (см. [3, гл.IV])
(см. [3, гл.IV])
и нормированные условием
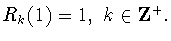 Как известно (см.
[4, с.75]), они удовлетворяют рекуррентному соотношению
при k=1,2,...
Как известно (см.
[4, с.75]), они удовлетворяют рекуррентному соотношению
при k=1,2,...
Ясно, что система косинус-полиномов Якоби
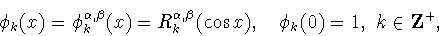 |
(1.1) |
является ортогональной на
отрезке ![$[0,\pi]$](img14.gif) c весом
c весом
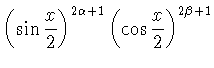
Приведем известные примеры таких
полиномов (см. [3, с.72, (4.1.7), (4.1.8)])
Косинус-полиномы Якоби
обладают следующими замечательными свойствами (см. [3, с.71,
(4.1.5)]): при любых
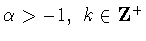 справедливы равенства
справедливы равенства
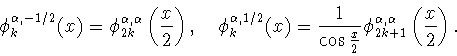 |
(1.2) |
Обозначим через
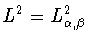 пространство
вещественных измеримых четных
пространство
вещественных измеримых четных  -периодических функций вида
-периодических функций вида
 со скалярным произведением
со скалярным произведением
и нормой
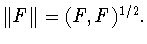 Наилучшим приближением функции
Наилучшим приближением функции 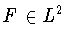 пространством
пространством
косинус-полиномов порядка 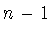 называется
величина
называется
величина
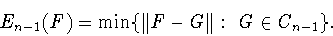 |
(1.3) |
Для оценки сверху этой величины нам понадобится важное
обобщение понятия сдвига (см. [5]) произвольной функции
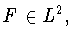 основанное на ее разложении в ряд Фурье по
косинус-полиномам Якоби
основанное на ее разложении в ряд Фурье по
косинус-полиномам Якоби
 |
(1.4) |
А именно,
оператором (обобщенного) сдвига с шагом 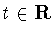 называется
линейный оператор
называется
линейный оператор 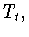 который действует на функции
который действует на функции 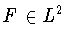 вида (1.4) по закону
вида (1.4) по закону
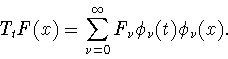 |
(1.5) |
Поскольку 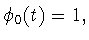 то, как нетрудно заметить, оператор сдвига
(с любым фиксированным шагом
то, как нетрудно заметить, оператор сдвига
(с любым фиксированным шагом 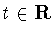 ) переводит постоянные
функции в себя, например,
) переводит постоянные
функции в себя, например, 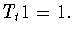 Кроме того, известно (см.
[3, с.175, (7.32.2)]), что в случае
Кроме того, известно (см.
[3, с.175, (7.32.2)]), что в случае
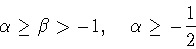 |
(1.6) |
косинус-полиномы
Якоби
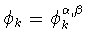 удовлетворяют следующим
соотношениям
удовлетворяют следующим
соотношениям
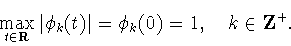 |
(1.7) |
Следовательно,
в этом случае норма оператора 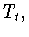 как оператора из
как оператора из 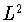 в
в
 равна единице. Поэтому применима схема Грюнвальда -
Летникова [6], [7] (см. также
[8, § 20], [9], [10]) построения
соответствующего разностного оператора (вещественного) порядка
равна единице. Поэтому применима схема Грюнвальда -
Летникова [6], [7] (см. также
[8, § 20], [9], [10]) построения
соответствующего разностного оператора (вещественного) порядка
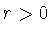 с шагом
с шагом 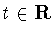
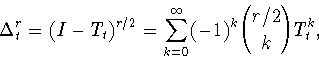 |
(1.8) |
где  - тождественный оператор,
- тождественный оператор,
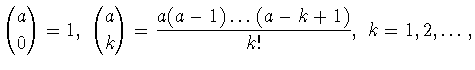 - биномиальные коэффициенты. Модулем непрерывности порядка
- биномиальные коэффициенты. Модулем непрерывности порядка  функции
функции  называется следующая функция переменного
называется следующая функция переменного 
Следующая взаимосвязь между модулями непрерывности различных
порядков получается путем повторения рассуждений, содержащихся в
работах С.Б.Стечкина [11, лемма 2], Х.П.Рустамова
[9, с.130, неравенство (1.8) и его обоснование]. Пусть
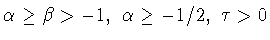 . Тогда для любой
функции
. Тогда для любой
функции
 выполняется неравенство
выполняется неравенство
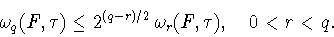 |
(1.9) |
Кроме того, из определений (1.8),
(1.5) и равенства Парсеваля следует, что для каждой функции
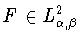 вида (1.4) справедливо соотношение
вида (1.4) справедливо соотношение
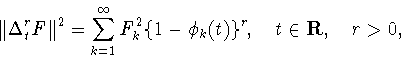 |
(1.10) |
из которого следует, что при 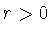
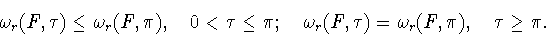 |
(1.11) |
Зафиксируем числа 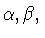 удовлетворяющие условиям
(1.6), а также числа
удовлетворяющие условиям
(1.6), а также числа 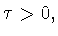
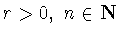 и
рассмотрим классическую задачу о точной константе
и
рассмотрим классическую задачу о точной константе
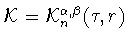 в неравенстве Джексона-Стечкина в
пространстве
в неравенстве Джексона-Стечкина в
пространстве
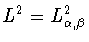
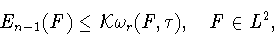 |
(1.12) |
т.е. задачу о
вычислении величины
 |
(1.13) |
Величину (1.13) мы будем иногда
называть константой Джексона-Стечкина. Эта задача имеет большую
историю, информация о качественной картине в этой области (вопросы
ограниченности констант) содержится в работах М.К.Потапова
[12], Х.П.Рустамова [10]. Что касается точных
результатов в этой тематике, то соответствующие исторические
сведения можно найти в работе автора [1]. Ниже мы
перечислим лишь те из них, которые имеют непосредственное отношение
к теме исследований данной статьи. Хотя некоторые авторы приводимых
ниже результатов применяли иные модули непрерывности, но при
доказательстве они переходили к задачам, которые возникают и в
данной работе. Учитывая это обстоятельство, мы сформулируем
указанные результаты в обозначениях, принятых здесь.
Точную константу в неравенстве Джексона-Стечкина (1.12) в
пространстве
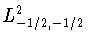 нашел Н.И.Черных в 1967 году
[13]
нашел Н.И.Черных в 1967 году
[13]
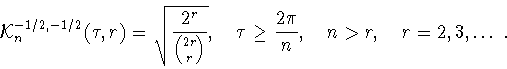 |
(1.14) |
Для
случая  он получил [14],
[15] более тонкое утверждение относительно
поведения величины
он получил [14],
[15] более тонкое утверждение относительно
поведения величины
 по
по 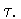 Подробнее, Н.И.Черных нашел точку
Подробнее, Н.И.Черных нашел точку

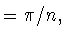 начиная с которой указанная величина выходит на
свой глобальный минимум, равный единице
начиная с которой указанная величина выходит на
свой глобальный минимум, равный единице
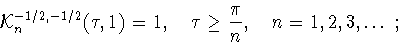 |
(1.15) |
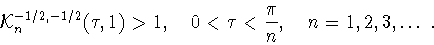 |
(1.16) |
Положим
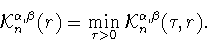 |
(1.17) |
Используя определение (1.13) и
свойство (1.11), легко заметить, что
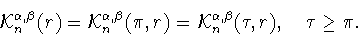 |
(1.18) |
Сейчас
естественно ввести следующее
Определение 1.1
Точкой Черныха в неравенстве Джексона-Стечкина (
1.12) в
пространстве
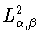
называется точная нижняя грань
положительных значений
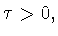
для которых величина
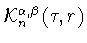
(как функция переменной
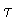
)
принимает свое минимальное значение
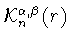
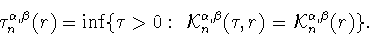 |
(1.19) |
Следующий существенный шаг в этом направлении был сделан В.А.Юдиным
[16], который получил точное неравенство Джексона (с первым
модулем непрерывности) в пространстве
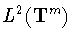 функций на
многомерном торе
функций на
многомерном торе
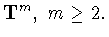 Ряд точных неравенств
Джексона-Стечкина между наилучшим среднеквадратичным приближением
функции (одной или нескольких переменных) и значением ее
Ряд точных неравенств
Джексона-Стечкина между наилучшим среднеквадратичным приближением
функции (одной или нескольких переменных) и значением ее 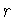 -го
модуля непрерывности в одной точке был получен в работах
[17], [18], [19], [20],
[21], [22], [23],
[24], [1], [25],
[](Gorbachev), [27]. В частности, в работе автора
[1, теоремы 2.1, 2.2, замечания 2.1 - 2.5] содержится
результат (см. теорему 1.1 ниже), относящийся к
ультрасферическому случаю задачи (1.13) о точной константе в
неравенстве Джексона-Стечкина (1.12) в пространстве
-го
модуля непрерывности в одной точке был получен в работах
[17], [18], [19], [20],
[21], [22], [23],
[24], [1], [25],
[](Gorbachev), [27]. В частности, в работе автора
[1, теоремы 2.1, 2.2, замечания 2.1 - 2.5] содержится
результат (см. теорему 1.1 ниже), относящийся к
ультрасферическому случаю задачи (1.13) о точной константе в
неравенстве Джексона-Стечкина (1.12) в пространстве
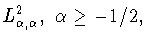 который тесно связан с
аналогичной задачей в пространстве
который тесно связан с
аналогичной задачей в пространстве
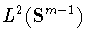 функций на
единичной сфере
функций на
единичной сфере 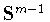 вещественного евклидова
пространства
вещественного евклидова
пространства  размерности
размерности 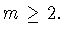
При
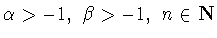 обозначим через
обозначим через
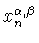 первый положительный нуль
косинус-полинома Якоби
первый положительный нуль
косинус-полинома Якоби
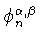 (см. (1.1))
(см. (1.1))
 |
(1.20) |
Замечание 1.1.
1) Пункт (B) теоремы 1.1 принадлежит В.В.Арестову,
который на самом деле установил более общее утверждение
[24, теорема 1], [1, лемма 4.2].
2) Для
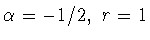 утверждения теоремы 1.1 получены
Н.И.Черных [14].
утверждения теоремы 1.1 получены
Н.И.Черных [14].
3) При
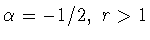 неравенство (1.21) доказано
В.В.Шалаевым [22].
неравенство (1.21) доказано
В.В.Шалаевым [22].
4) В случаях
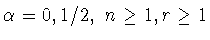 В.Ю.Попов получил
неравенство [24, (6.4), (6.6)]
В.Ю.Попов получил
неравенство [24, (6.4), (6.6)]
которое при
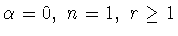 и
и
 совпадает с неравенством
(1.21), а при
совпадает с неравенством
(1.21), а при
 неравенство
(1.21) уточняет указанный результат В.Ю.Попова, т.к.
неравенство
(1.21) уточняет указанный результат В.Ю.Попова, т.к.
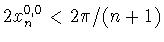 (см. [3, с.147, (6.6.4)]).
(см. [3, с.147, (6.6.4)]).
5) В силу известного свойства (1.9) модуля непрерывности
первое неравенство в пункте (A) влечет второе. В работе
[1] содержится также иное доказательство неравенства
(1.22).
Замечание 1.2.
Ниже (см. первое утверждение
следствия 4.1) будет показано, что утверждение (B) теоремы 1.1
выполняется и при 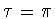 (а значит, и при любом
(а значит, и при любом 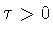 ).
).
Предложение 1.1
Если
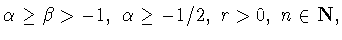
то с помощью функции
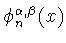
легко
показать (см. (
1.10), (
3.1)), что при
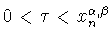
точная константа
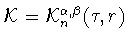
в неравенстве (
1.12) будет
строго больше единицы
Теорема 1.1, замечание 1.2 и предложение 1.1
позволяют локализовать точку Черныха (1.19) в неравенстве
Джексона-Стечкина (1.12) в пространстве
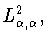 при
при
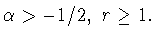
Следствие 1.1
Пусть
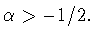
Тогда точная константа в неравенстве
Джексона-Стечкина (
1.12) в пространстве
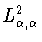
удовлетворяет соотношениям
и потому
имеют место оценки



Next: 2. Формулировка основного результата.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
![]() и
и
![]() -
алгебраические многочлены Якоби порядка
-
алгебраические многочлены Якоби порядка
![]() ортогональные на отрезке
ортогональные на отрезке ![]() c весом
c весом
![]() (см. [3, гл.IV])
(см. [3, гл.IV]) 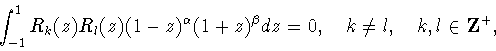


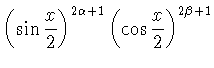

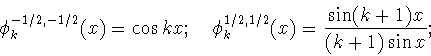
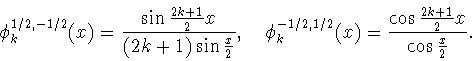
![]() пространство
вещественных измеримых четных
пространство
вещественных измеримых четных ![]() -периодических функций вида
-периодических функций вида
![]() со скалярным произведением
со скалярным произведением 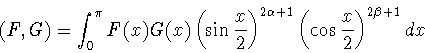
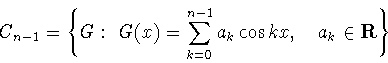
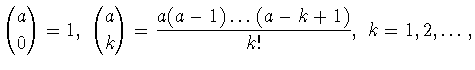 - биномиальные коэффициенты. Модулем непрерывности порядка
- биномиальные коэффициенты. Модулем непрерывности порядка ![]() . Тогда для любой
функции
. Тогда для любой
функции
![]() выполняется неравенство
выполняется неравенство
![]() удовлетворяющие условиям
(1.6), а также числа
удовлетворяющие условиям
(1.6), а также числа ![]()
![]() и
рассмотрим классическую задачу о точной константе
и
рассмотрим классическую задачу о точной константе
![]() в неравенстве Джексона-Стечкина в
пространстве
в неравенстве Джексона-Стечкина в
пространстве
![]()
![]() нашел Н.И.Черных в 1967 году
[13]
нашел Н.И.Черных в 1967 году
[13] ![]() функций на
многомерном торе
функций на
многомерном торе
![]() Ряд точных неравенств
Джексона-Стечкина между наилучшим среднеквадратичным приближением
функции (одной или нескольких переменных) и значением ее
Ряд точных неравенств
Джексона-Стечкина между наилучшим среднеквадратичным приближением
функции (одной или нескольких переменных) и значением ее ![]() -го
модуля непрерывности в одной точке был получен в работах
[17], [18], [19], [20],
[21], [22], [23],
[24], [1], [25],
[](Gorbachev), [27]. В частности, в работе автора
[1, теоремы 2.1, 2.2, замечания 2.1 - 2.5] содержится
результат (см. теорему 1.1 ниже), относящийся к
ультрасферическому случаю задачи (1.13) о точной константе в
неравенстве Джексона-Стечкина (1.12) в пространстве
-го
модуля непрерывности в одной точке был получен в работах
[17], [18], [19], [20],
[21], [22], [23],
[24], [1], [25],
[](Gorbachev), [27]. В частности, в работе автора
[1, теоремы 2.1, 2.2, замечания 2.1 - 2.5] содержится
результат (см. теорему 1.1 ниже), относящийся к
ультрасферическому случаю задачи (1.13) о точной константе в
неравенстве Джексона-Стечкина (1.12) в пространстве
![]() который тесно связан с
аналогичной задачей в пространстве
который тесно связан с
аналогичной задачей в пространстве
![]() функций на
единичной сфере
функций на
единичной сфере ![]() вещественного евклидова
пространства
вещественного евклидова
пространства ![]() размерности
размерности ![]()
![]() обозначим через
обозначим через
![]() первый положительный нуль
косинус-полинома Якоби
первый положительный нуль
косинус-полинома Якоби
![]() (см. (1.1))
(см. (1.1))
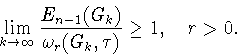
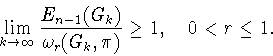
![]() утверждения теоремы 1.1 получены
Н.И.Черных [14].
утверждения теоремы 1.1 получены
Н.И.Черных [14].
![]() неравенство (1.21) доказано
В.В.Шалаевым [22].
неравенство (1.21) доказано
В.В.Шалаевым [22].
![]() В.Ю.Попов получил
неравенство [24, (6.4), (6.6)]
В.Ю.Попов получил
неравенство [24, (6.4), (6.6)] 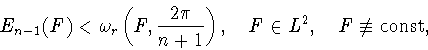
![]() (а значит, и при любом
(а значит, и при любом ![]() ).
).
![]() при
при
![]()