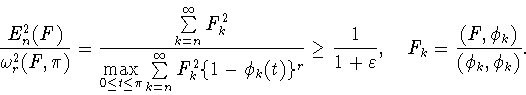Next: 4. Неравенство Джексона-Стечкина в
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: 2. Формулировка основного результата.
Пусть
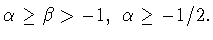 По
стандартной схеме (см., например, [1]), с помощью
равенства Парсеваля, получаем, что для любой функции
По
стандартной схеме (см., например, [1]), с помощью
равенства Парсеваля, получаем, что для любой функции
 квадрат величины (1.3) ее наилучшего
среднеквадратичного приближения косинус-полиномами порядка
квадрат величины (1.3) ее наилучшего
среднеквадратичного приближения косинус-полиномами порядка 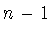 вычисляется по формуле
вычисляется по формуле
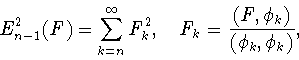 |
(3.1) |
где
 -
косинус-полиномы Якоби (1.1), а квадрат нормы ее разности
порядка
-
косинус-полиномы Якоби (1.1), а квадрат нормы ее разности
порядка 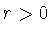 с шагом
с шагом 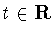 удовлетворяет равенству
(1.10). Поэтому задача (1.13) сводится к следующей
экстремальной задаче для косинус-полиномов Якоби. При фиксированных
удовлетворяет равенству
(1.10). Поэтому задача (1.13) сводится к следующей
экстремальной задаче для косинус-полиномов Якоби. При фиксированных
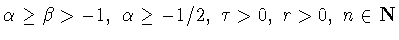 найти наилучшую константу
найти наилучшую константу
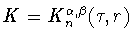 в
неравенстве
в
неравенстве
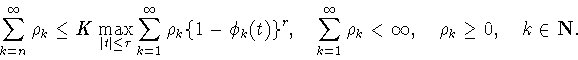 |
(3.2) |
Не трудно показать, что
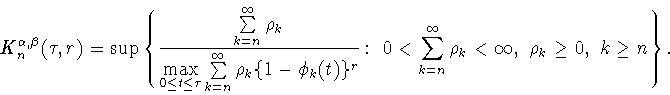 |
(3.3) |
Обратим внимание читателя на то, что суммирование во
всех суммах в (3.3) ведется по 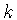 , начиная с
, начиная с 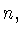 и это не
есть опечатка. Очевидно также, что справедливо равенство
и это не
есть опечатка. Очевидно также, что справедливо равенство
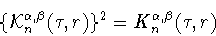 |
(3.4) |
при
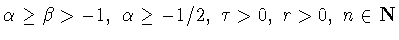 . Задачу (3.3) можно
преобразовать к виду
. Задачу (3.3) можно
преобразовать к виду
![\begin{displaymath}
K_{n}^{\alpha,\beta}(\tau,r)=\sup\left\{
\sum\limits_{k=n}^{...
...(t)\}^r\le 1, \ t\in
[0,\tau];\ \rho_k\ge 0,\ k\ge n \right\}. \end{displaymath}](img155.gif) |
(3.5) |
Видно, что
(3.5) есть задача (бесконечномерного) линейного
программирования. Такого рода задачи возникают и в других областях
математики, например, при исследовании границ упаковок некоторых
метрических пространств по схеме Дельсарта ([28],
[29], [30], [4], [31, гл.9, 13,
14], [25]), оценок снизу мощности дизайнов
(см. [32]), а также в теории чисел (см. [33],
[34] и приведенную там библиографию).
Для оценки снизу величины (3.3) нам понадобится следующее
утверждение, доказанное В.В.Арестовым [24, теорема
1], [1, лемма 4.2]. Ниже мы будем
использовать стандартное обозначение
![$\Vert f\Vert _{C[a,b]}=\max\limits_{x\in[a,b]}\vert f(x)\vert$](img156.gif) равномерной нормы
непрерывной на отрезке
равномерной нормы
непрерывной на отрезке ![$[a,b]$](img157.gif) функции
функции 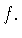
Лемма 3.1
(В.В.Арестов).
Пусть на отрезке
![$[ 0, \tau],\ \tau>0,$](img159.gif)
задана система непрерывных функций
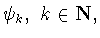
удовлетворяющая следующим условиям:
1)
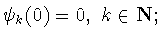
2)
![$\sup\limits_{k\in{\bf N}}\Vert\psi_k\Vert _{C[0,\tau]}<\infty;$](img162.gif)
3) для любого
![$\xi \in (0,\tau]$](img163.gif)
выполняется неравенство
Тогда для любого
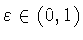
найдется функция
с неотрицательными коэффициентами

такая, что
Следствие 3.1
Пусть
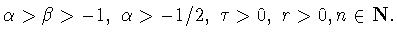
Тогда для точной константы
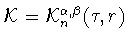
(см. (
1.13)) в неравенстве
Джексона-Стечкина (
1.12) в пространстве
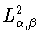
имеет место следующая оценка снизу
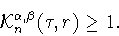 |
(3.6) |
Доказательство. Из определения (1.17) и соотношения
(1.18) вытекает, что неравенство (3.6) достаточно
доказать при 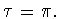 Известно (см. [3, § 7.32.]), что
при
Известно (см. [3, § 7.32.]), что
при
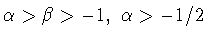 косинус-полиномы Якоби
(1.1)
косинус-полиномы Якоби
(1.1)
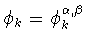 для произвольного
фиксированного
для произвольного
фиксированного
![$\xi\in (0,\pi]$](img174.gif) равномерно стремятся к нулю на
отрезке
равномерно стремятся к нулю на
отрезке ![$[\xi,\pi]$](img175.gif) , т.е.
, т.е.
Отсюда, с учетом свойства
(1.7), следует, что при каждом фиксированном 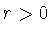 система
функций
система
функций
удовлетворяет условиям леммы 3.1 при 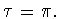 И значит,
для любого
И значит,
для любого
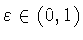 найдется функция
найдется функция
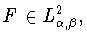 такая, что
такая, что
Это соотношение и определение (1.13) влекут (3.6).
Следствие доказано.



Next: 4. Неравенство Джексона-Стечкина в
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: 2. Формулировка основного результата.
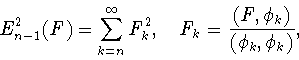
![]() равномерной нормы
непрерывной на отрезке
равномерной нормы
непрерывной на отрезке ![]() функции
функции ![]()
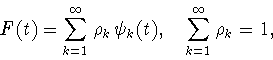
![]() Известно (см. [3, § 7.32.]), что
при
Известно (см. [3, § 7.32.]), что
при
![]() косинус-полиномы Якоби
(1.1)
косинус-полиномы Якоби
(1.1)
![]() для произвольного
фиксированного
для произвольного
фиксированного
![]() равномерно стремятся к нулю на
отрезке
равномерно стремятся к нулю на
отрезке ![]() , т.е.
, т.е.