- (A)
- для каждого натурального
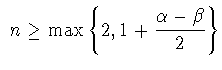 и
произвольной функции
и
произвольной функции 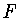 из пространства
из пространства
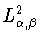 справедливы неравенства
справедливы неравенства
- (B)
- для каждого натурального числа
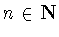 и любого
положительного числа
и любого
положительного числа 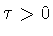 существует последовательность функций
существует последовательность функций
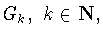 из
из
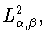 такая, что
такая, что
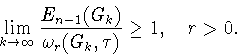
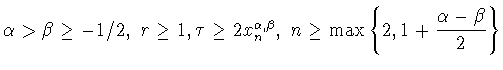 при
при
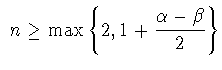 и
произвольной функции
и
произвольной функции 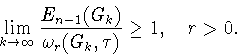
Замечание 2.1. Пункты 1), 5) замечания 1.1 остаются в силе и для теоремы 2.1.
Замечание 2.2.
Ниже (см. следствие 4.1) будет показано, что при
![]() утверждение
утверждение ![]() теоремы 2.1 справедливо для любого
натурального
теоремы 2.1 справедливо для любого
натурального ![]()
Замечание 2.3.
В случае
![]() утверждения теоремы 2.1
были анонсированы автором [2]
в иной эквивалентной форме.
утверждения теоремы 2.1
были анонсированы автором [2]
в иной эквивалентной форме.
С помощью теоремы 2.1, замечания 2.2 и предложения 1.1 получаем
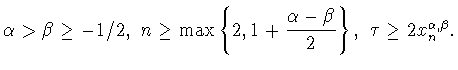 Тогда для точной константы (1.13) и
точки Черныха (1.19) в неравенстве Джексона-Стечкина
(1.12) в пространстве
Тогда для точной константы (1.13) и
точки Черныха (1.19) в неравенстве Джексона-Стечкина
(1.12) в пространстве
Доказательство теоремы 2.1 будет проведено поэтапно. Вначале мы покажем, как из результата В.В.Арестова [24, теорема 1], [1, лемма 4.2] и известных свойств полиномов Якоби следует оценка снизу для величины (1.13), а затем, применяя идеи, содержащиеся в работах Н.И. Черных [13], [14] и В.А.Юдина [16], по аналогии с тем, как это уже делалось в ультрасферическом случае в статье автора [1], построим вес (допустимую функцию в двойственной задаче), который даст нужную оценку сверху для искомой величины.