


Next: 7. Оценка сверху.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: 5. Двойственная задача.
В данном пункте
приводятся известные свойства обобщенного сдвига 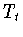 (см.
(1.5)), действующего в пространстве
(см.
(1.5)), действующего в пространстве
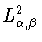 при
при
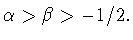 Отметим, что в ультрасферическом случае
Отметим, что в ультрасферическом случае
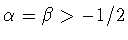 важные свойства этого сдвига были установлены в
1817 году А.М.Лежандром (случай
важные свойства этого сдвига были установлены в
1817 году А.М.Лежандром (случай
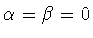 ) [41, с.262,
формула (
) [41, с.262,
формула (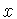 )] и в 1874 году - Л.Гегенбауэром (случай
)] и в 1874 году - Л.Гегенбауэром (случай
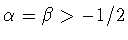 ) (см. [42, с.402]). А именно, ими была
доказана так называемая формула умножения для ультрасферических
полиномов
) (см. [42, с.402]). А именно, ими была
доказана так называемая формула умножения для ультрасферических
полиномов
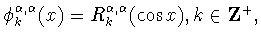
Почти сто лет спустя Дж.Гаспер получил аналог этого результата для
косинус-полиномов Якоби
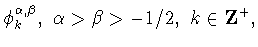 в следующей истокообразной форме
[35], [36] (см. также [38, пункт 5])
в следующей истокообразной форме
[35], [36] (см. также [38, пункт 5])
здесь 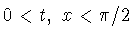 и ядро
и ядро
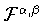 задается формулой
задается формулой
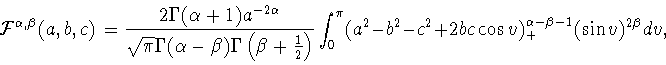 |
(6.3) |
Затем Т.Курнвиндер [37], [38]
(см. также [39, пункты 4,5]) нашел эквивалентное
выражение формулы умножения для косинус-полиномов Якоби
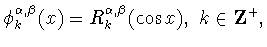 по форме более близкой к формуле умножения Лежандра - Гегенбауэра (6.1)
по форме более близкой к формуле умножения Лежандра - Гегенбауэра (6.1)
здесь
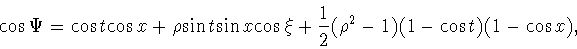 |
(6.5) |
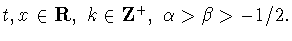 Следовательно, в этом случае действие сдвига (1.5) на произвольную
функцию
Следовательно, в этом случае действие сдвига (1.5) на произвольную
функцию
 при
при
 выражается в следующей интегральной форме
выражается в следующей интегральной форме
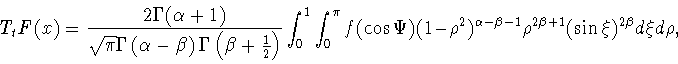 |
(6.6) |
где 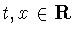 и
и 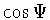 вычисляется по формуле (6.5).
Другое эквивалентное истокообразное представление этого сдвига получается с
помощью ядра (6.3) в формуле умножения (6.2)
[38, пункт 5], [39, пункт 4].
вычисляется по формуле (6.5).
Другое эквивалентное истокообразное представление этого сдвига получается с
помощью ядра (6.3) в формуле умножения (6.2)
[38, пункт 5], [39, пункт 4].
Необходимо сказать, что указанным выше результатам Дж.Гаспера и
Т.Курнвиндера, как отмечается в работе [37],
предшествовал результат Р.Л.Шапиро [40] (1968 г.) о
формуле сложения для полиномов Якоби, из которого следует
(6.6) при
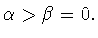
Приведем несколько свойств сдвига, вытекающих из его интегрального
представления. Эти свойства нам потребуются в следующем пункте.
Лемма 6.1
Пусть
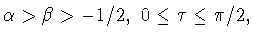
функция

непрерывна при всех
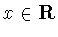
и
Тогда функция
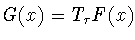
является непрерывной при всех
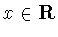
и
Доказательство.
Непрерывность функции 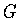 легко следует из интегрального представления
(6.6), (6.5) оператора сдвига.
По условию леммы имеем
легко следует из интегрального представления
(6.6), (6.5) оператора сдвига.
По условию леммы имеем
В силу интегрального представления (6.6), (6.5) сдвига для
доказательства леммы достаточно показать, что функция
удовлетворяет неравенствам
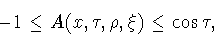 |
(6.7) |
если выполнены условия
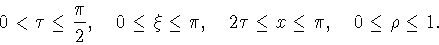 |
(6.8) |
Вначале докажем первое неравенство в (6.7). Ясно, что из (6.8)
следует, что
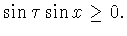 Поэтому имеем
Поэтому имеем
Заметим, что функция
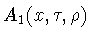 по третьей переменной
по третьей переменной  является параболой, причем ее глобальный минимум по этому аргументу
достигается в точке
является параболой, причем ее глобальный минимум по этому аргументу
достигается в точке
То есть
и, значит, первое неравенство в (6.7) доказано.
Перейдем к доказательству второго неравенства в (6.7).
Условия (6.8) влекут неравенство
а также
Имеем
Лемма доказана.
В работе Дж.Гаспера [35] содержится следующее
определение свертки двух функций 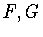 из
из
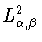 (а на самом
деле - и для функций из
(а на самом
деле - и для функций из
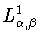 ), которое можно записать в
виде
), которое можно записать в
виде
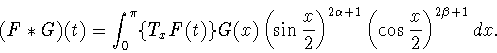 |
(6.9) |
Кроме того, в указанной работе приведено свойство коммутативности этой
операции
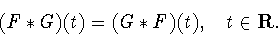 |
(6.10) |
Поскольку
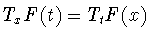 для любых
для любых
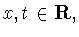 то равенство
(6.10) означает самосопряженность оператора сдвига. То есть
справедлива лемма.
то равенство
(6.10) означает самосопряженность оператора сдвига. То есть
справедлива лемма.
Лемма 6.2
Пусть
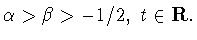
Тогда для любых двух функций
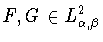
выполняется равенство
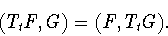 |
(6.11) |



Next: 7. Оценка сверху.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: 5. Двойственная задача.
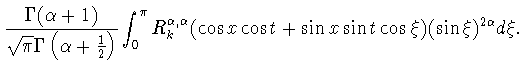
![]() в следующей истокообразной форме
[35], [36] (см. также [38, пункт 5])
в следующей истокообразной форме
[35], [36] (см. также [38, пункт 5])
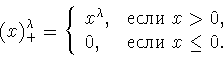
![]() по форме более близкой к формуле умножения Лежандра - Гегенбауэра (6.1)
по форме более близкой к формуле умножения Лежандра - Гегенбауэра (6.1)
![]()
![]() легко следует из интегрального представления
(6.6), (6.5) оператора сдвига.
По условию леммы имеем
легко следует из интегрального представления
(6.6), (6.5) оператора сдвига.
По условию леммы имеем
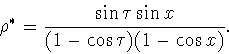
![]() из
из
![]() (а на самом
деле - и для функций из
(а на самом
деле - и для функций из
![]() ), которое можно записать в
виде
), которое можно записать в
виде