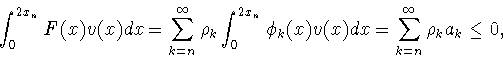Next: 8. Доказательство теоремы 2.1.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: 6. Некоторые свойства обобщенного
В данном пункте будет построен вес
![$\mu\in V_0^+[0,\tau],$](img266.gif) на котором, при
выполнении условий (5.5), достигается минимум в двойственной задаче
(5.2).
на котором, при
выполнении условий (5.5), достигается минимум в двойственной задаче
(5.2).
Рассмотрим следующее множество функций
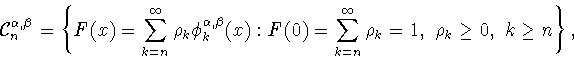 |
(7.1) |
где
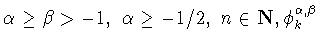 - косинус-полином Якоби (1.1). Это
множество является выпуклым подмножеством пространства
- косинус-полином Якоби (1.1). Это
множество является выпуклым подмножеством пространства ![$C[0,\pi]$](img269.gif) непрерывных на
непрерывных на ![$[0,\pi]$](img14.gif) функций. Так же, как и в ультрасферическом
случае [1, пункт 4], введем следующее
функций. Так же, как и в ультрасферическом
случае [1, пункт 4], введем следующее
Результаты Н.И.Черных [14],
[15] (см. (1.15), (1.16)) эквивалентны
равенству
В.Ю.Попов [17, теорема 3] получил
результат, из которого вытекает неравенство
В работе автора
[1, лемма 4.1] получены оценки
С помощью функции
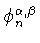 легко доказать
следующее утверждение.
легко доказать
следующее утверждение.
Предложение 7.1
При
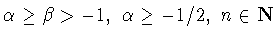
имеет
место оценка снизу
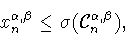 |
(7.2) |
где
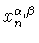
есть первый
положительный нуль косинус-полинома Якоби
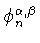
(см. (
1.20)).
В дальнейшем нам потребуются известные оценки для
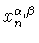 (см. [3, § 6.2]).
(см. [3, § 6.2]).
Основным результатом данного пункта является
Лемма 7.1
Пусть
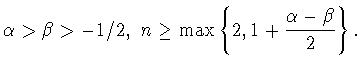
Тогда справедлива оценка сверху
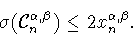 |
(7.3) |
Доказательство. Доказательство будем проводить так же, как
это сделано в ультрасферическом случае [1, лемма 4.1],
внеся естественные изменения. Для краткости положим
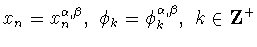 . Пусть
. Пусть
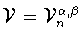 есть четная
есть четная
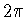 -периодическая функция, непрерывная на всей действительной
оси
-периодическая функция, непрерывная на всей действительной
оси 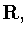 которую достаточно задать на отрезке
которую достаточно задать на отрезке ![$[0,\pi]:$](img294.gif)
 |
(7.4) |
Определим четную 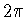 -периодическую функцию
-периодическую функцию 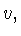 задав ее на
отрезке
задав ее на
отрезке ![$[0,\pi]$](img14.gif) формулой
формулой
![\begin{displaymath}
v(x)=\left(\sin\frac{x}{2}\right)^{2\alpha+1}
\left(\cos\frac{x}{2}\right)^{2\beta+1} T_{x_n}{\cal V}(x), \quad
x\in[0,\pi], \end{displaymath}](img297.gif) |
(7.5) |
где 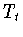 есть оператор (обобщенного) сдвига с
шагом
есть оператор (обобщенного) сдвига с
шагом 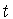 (см. (1.5), (6.6)). Из определения (7.4),
предложения 7.2, леммы 6.1 и формулы (6.6)
следует, что
(см. (1.5), (6.6)). Из определения (7.4),
предложения 7.2, леммы 6.1 и формулы (6.6)
следует, что
![\begin{displaymath}
v(x)\ge 0,\quad x\in{\bf R};\quad
v(x)\not\equiv 0;\quad v(x)=0,\quad x\in[2x_n^{\alpha,\beta},\pi].
\end{displaymath}](img299.gif) |
(7.6) |
Используя самосопряженность оператора сдвига (см.
лемму 6.2) найдем следующие коэффициенты
где
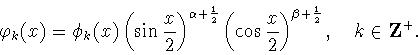 |
(7.8) |
Функции 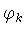 удовлетворяют дифференциальному уравнению
(см. [3, с.79,§ 4.24])
удовлетворяют дифференциальному уравнению
(см. [3, с.79,§ 4.24])
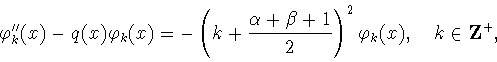 |
(7.9) |
где
Рассмотрим выражение
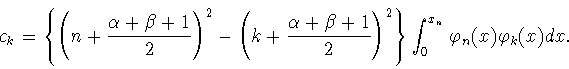 |
(7.10) |
С помощью уравнения (7.9) получаем
Из (7.7) -
(7.11) видно, что
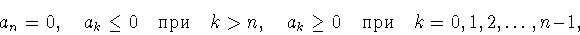 |
(7.12) |
так как
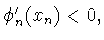 и при
и при 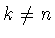 имеем
имеем
Учитывая свойства (7.6) и
(7.12), получаем, что для каждой функции
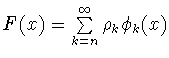 из множества
из множества
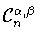 (см. (7.1)) выполняется соотношение
(см. (7.1)) выполняется соотношение
и, значит, найдется точка
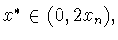 в которой
в которой 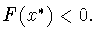 Отсюда
следует (7.3). Лемма доказана.
Отсюда
следует (7.3). Лемма доказана.



Next: 8. Доказательство теоремы 2.1.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: 6. Некоторые свойства обобщенного
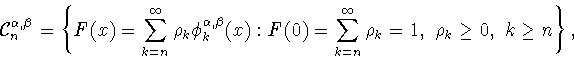
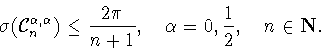
![]() (см. [3, § 6.2]).
(см. [3, § 6.2]).
![]() . Пусть
. Пусть
![]() есть четная
есть четная
![]() -периодическая функция, непрерывная на всей действительной
оси
-периодическая функция, непрерывная на всей действительной
оси ![]() которую достаточно задать на отрезке
которую достаточно задать на отрезке ![]()

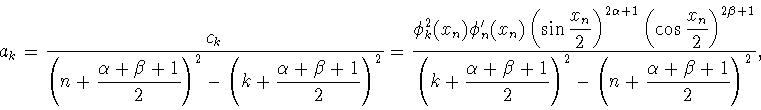
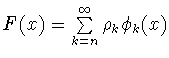 из множества
из множества
![]() (см. (7.1)) выполняется соотношение
(см. (7.1)) выполняется соотношение