


Next: 6. Некоторые свойства обобщенного
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА ДЛЯ
Previous: 4. Неравенство Джексона-Стечкина в
Большую роль при исследовании задачи
(1.13) или эквивалентной ей задачи (3.3), (3.5)
играет двойственная задача, которая для случая
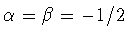 ,
по существу, содержится и успешно применена в 1967 г. Н.И.Черных
[14], [13]. Соотношение
двойственности для более общей, чем (3.3), задачи было явно
сформулировано и обосновано в совместной работе В.В.Арестова и
В.Ю.Попова [24, леммы 1,2], которое мы приведем
(для задачи (3.3)) в форме, близкой к той, которую использовал
автор в [20, теорема 1] в случае
,
по существу, содержится и успешно применена в 1967 г. Н.И.Черных
[14], [13]. Соотношение
двойственности для более общей, чем (3.3), задачи было явно
сформулировано и обосновано в совместной работе В.В.Арестова и
В.Ю.Попова [24, леммы 1,2], которое мы приведем
(для задачи (3.3)) в форме, близкой к той, которую использовал
автор в [20, теорема 1] в случае
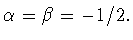
Именно, пусть
![$\tau>0,\ V^+_0=V^+_0[0,\tau]$](img190.gif) - множество ограниченных,
неубывающих на отрезке
- множество ограниченных,
неубывающих на отрезке ![$[0,\tau]$](img191.gif) функций
функций
 непрерывных в нуле
непрерывных в нуле
 Такие функции
Такие функции 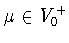 будем называть весами.
будем называть весами.
Лемма 5.1
Пусть выполнены условия
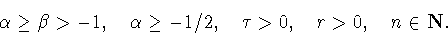 |
(5.1) |
Тогда
для величины (
3.3) имеет место равенство
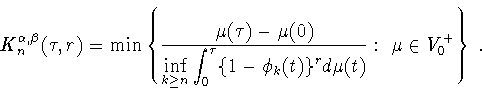 |
(5.2) |
Из этой леммы следует, что каждый вес 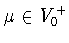 дает
для величины (3.3), а следовательно
(см. (3.4)), и для искомой величины (1.13), оценки сверху
дает
для величины (3.3), а следовательно
(см. (3.4)), и для искомой величины (1.13), оценки сверху
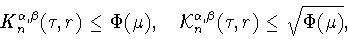 |
(5.3) |
где функционал
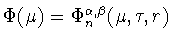 задается формулой
задается формулой
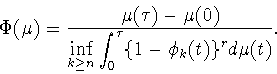 |
(5.4) |
Ниже (в пункте 6) при
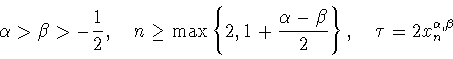 |
(5.5) |
будет построен вес
![$\mu = \mu_{\tau} \in
V_0^+[0,\tau]$](img202.gif) , на котором значение функционала (5.4) равно
единице
, на котором значение функционала (5.4) равно
единице
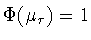 . И, значит, (см. (5.3)) в этом
случае мы получим оценку сверху для величины (1.13),
совпадающую с оценкой снизу (3.6), т.е. найдем величину
. И, значит, (см. (5.3)) в этом
случае мы получим оценку сверху для величины (1.13),
совпадающую с оценкой снизу (3.6), т.е. найдем величину
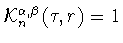 при выполнении
условий (5.5). Для построения указанного веса нам понадобятся
некоторые известные свойства обобщенного сдвига, вытекающие из его
интегрального представления, которое, в свою очередь, следует из
формулы умножения для полиномов Якоби
при выполнении
условий (5.5). Для построения указанного веса нам понадобятся
некоторые известные свойства обобщенного сдвига, вытекающие из его
интегрального представления, которое, в свою очередь, следует из
формулы умножения для полиномов Якоби
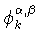 при
при
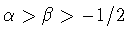 , установленной
Дж. Гаспером [35], [36], а затем доказанной в
другой эквивалентной форме
Т. Курнвиндером [37], [38] (см.
также [39, (4.2), (5.4), (5.5)]). При этом, как
отмечается в [37], в случае
, установленной
Дж. Гаспером [35], [36], а затем доказанной в
другой эквивалентной форме
Т. Курнвиндером [37], [38] (см.
также [39, (4.2), (5.4), (5.5)]). При этом, как
отмечается в [37], в случае
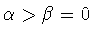 формула
сложения (и, как следствие, формула умножения) для полиномов Якоби
получена ранее Р.Л.Шапиро [40].
формула
сложения (и, как следствие, формула умножения) для полиномов Якоби
получена ранее Р.Л.Шапиро [40].
![]() - множество ограниченных,
неубывающих на отрезке
- множество ограниченных,
неубывающих на отрезке ![]() функций
функций
![]() непрерывных в нуле
непрерывных в нуле
![]() Такие функции
Такие функции ![]() будем называть весами.
будем называть весами.
![]() дает
для величины (3.3), а следовательно
(см. (3.4)), и для искомой величины (1.13), оценки сверху
дает
для величины (3.3), а следовательно
(см. (3.4)), и для искомой величины (1.13), оценки сверху