


Next: 5. Доказательство теоремы 2.1.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
Previous: 3. Некоторые свойства ультрасферического
Рассмотрим следующее множество функций
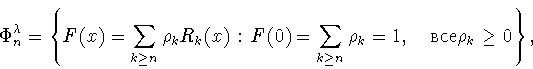 |
(4.1) |
где
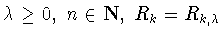 - косинус-полиномы
(3.4) Гегенбауэра. Это множество является выпуклым
подмножеством пространства
- косинус-полиномы
(3.4) Гегенбауэра. Это множество является выпуклым
подмножеством пространства ![$C[0, \pi]$](img321.gif) непрерывных на
непрерывных на ![$[0,\pi]$](img170.gif) функций.
функций.
ОПРЕДЕЛЕНИЕ 4.1.
Положительное число
 назовем точкой Черныха для
множества
назовем точкой Черныха для
множества
 если одновременно выполняются следующие два
условия
если одновременно выполняются следующие два
условия
- (a)
- для любой функции
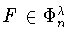 найдется точка
найдется точка
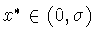 , в которой
, в которой
 ;
;
- (b)
- для любого
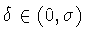 найдутся
функция
найдутся
функция
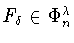 и число
и число
 , такие что
, такие что
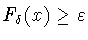 при всех
при всех
![$x \in [0, \delta ]$](img331.gif) .
.
Результаты (2.1), (2.2) Н.И. Черных эквивалентны равенству
 |
(4.2) |
В.Ю. Попов [25, теорема 3] получил результат, из
которого вытекает неравенство
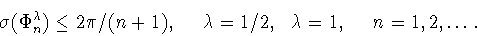 |
(4.3) |
Одним из основных результатов этого пункта является
ЛЕММА 4.1
Пусть
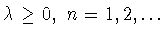
. Тогда
справедливы оценки
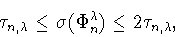 |
(4.4) |
где
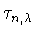
есть первый положительный нуль полинома
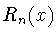
(см. (
3.4), (
2.5)).
ЗАМЕЧАНИЕ 4.1. При 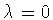 , в силу равенства
(4.2) Н.И. Черных,
, в силу равенства
(4.2) Н.И. Черных,
 . При
. При
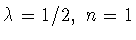 и при
и при
 оценка сверху в
(4.4) совпадает с неравенством (4.3) В.Ю. Попова,
а при
оценка сверху в
(4.4) совпадает с неравенством (4.3) В.Ю. Попова,
а при
 уточняет его, т.к.
уточняет его, т.к.
 (см. [40, с.147, (6.6.4)]).
(см. [40, с.147, (6.6.4)]).
Доказательство леммы 4.1. Оценка снизу
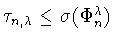 вытекает из того, что функция
вытекает из того, что функция 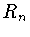 принадлежит
множеству
принадлежит
множеству
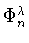 и удовлетворяет неравенству
и удовлетворяет неравенству
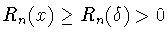 при всех
при всех
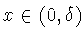 и
и
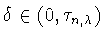 . Доказательство оценки сверху
. Доказательство оценки сверху
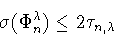 |
(4.5) |
будем проводить по схеме
Н.И. Черных [6]. А именно, построим вес -
неотрицательную, ненулевую и интегрируемую на
![$[0,2 \tau_{n,\lambda }]$](img347.gif) функцию
функцию
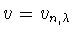 , удовлетворяющую условиям
, удовлетворяющую условиям
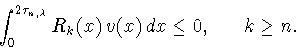 |
(4.6) |
Эти условия дадут нам неравенство (4.5), т.к. для каждой
функции
из
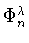 мы
имели бы
мы
имели бы
Отсюда, ввиду нетривиальности и неотрицательности 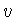 ,
следовало бы существование точки
,
следовало бы существование точки
 из
открытого интервала
из
открытого интервала
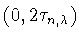 , в которой
, в которой  .
.
Идея построения искомого веса 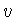 близка к той, которая применялась
В.А. Юдиным в работе [24]. Предварительно мы
определим четную
близка к той, которая применялась
В.А. Юдиным в работе [24]. Предварительно мы
определим четную 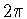 -периодическую непрерывную функцию
-периодическую непрерывную функцию
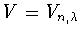 , которую достаточно задать на отрезке
, которую достаточно задать на отрезке ![$[0,\pi]$](img170.gif)
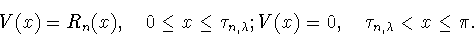 |
(4.7) |
Искомый вес
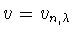 определим по формуле
определим по формуле
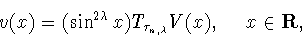 |
(4.8) |
где 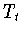 есть
(3.1) ультрасферический сдвиг с шагом
есть
(3.1) ультрасферический сдвиг с шагом 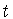 . Из определения
(3.1) видно, что
. Из определения
(3.1) видно, что 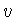 является ненулевой, неотрицательной и
непрерывной на замкнутом отрезке
является ненулевой, неотрицательной и
непрерывной на замкнутом отрезке ![$[0,\pi]$](img170.gif) функцией. При
функцией. При 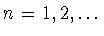 , в силу свойств (3.5)-(3.7), первый
положительный нуль полинома
, в силу свойств (3.5)-(3.7), первый
положительный нуль полинома 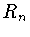 удовлетворяет неравенствам
удовлетворяет неравенствам
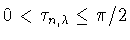 . Отсюда по лемме 3.1 имеем
. Отсюда по лемме 3.1 имеем
![\begin{displaymath}
v(x) = 0,\ \ \ x \in [2 \tau_{n,\lambda }, \pi]. \end{displaymath}](img359.gif) |
(4.9) |
Используя
(3.10) - самосопряженность оператора 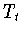 , получаем
, получаем
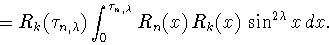 |
(4.10) |
Известно (см. [40, с.79]), что функции
удовлетворяют
уравнению
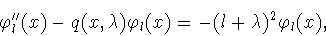 |
(4.11) |
Рассмотрим выражение
Применяя стандартный прием с использованием уравнения (4.11),
получим
Отсюда
и (4.10) вытекает, что
при 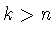 , т.к.
, т.к.
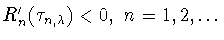 (поскольку все нули полинома
(поскольку все нули полинома 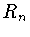 вещественные, простые и при переходе через точку
вещественные, простые и при переходе через точку
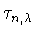 функция
функция 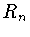 меняет знак с
меняет знак с 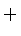 на
на 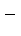 ). То есть мы нашли вес
). То есть мы нашли вес 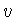 ,
удовлетворяющий условиям (4.6). Лемма доказана.
,
удовлетворяющий условиям (4.6). Лемма доказана.
Второе основное утверждение этого пункта принадлежит
В.В. Арестову и публикуется здесь с его разрешения.
ЛЕММА 4.2
Пусть на отрезке
![$[0, \tau]$](img377.gif)
задана система
непрерывных функций
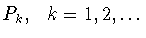
, удовлетворяющая
следующим трем условиям
- (a)
-
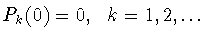 ;
;
- (b)
- существует абсолютная константа
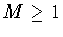 такая, что
такая, что
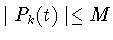 при
при
![$t \in [0,\tau],
k=1,2 ,\ldots $](img382.gif) ;
;
- (c)
- для любого
![$\xi \in (0, \tau]$](img383.gif) выполняется
неравенство
выполняется
неравенство
Тогда для любого
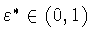
найдется функция
с неотрицательными коэффициентами
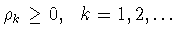
, такая, что
![\begin{displaymath}
F(t)\leq 1+\mbox{$\varepsilon$}^{\ast},\quad t \in [0,\tau]
\end{displaymath}](img388.gif) |
(4.12) |
ДОКАЗАТЕЛЬСТВО.
Возьмем
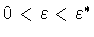 . Положим
. Положим
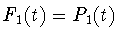 . Пусть построена функция
. Пусть построена функция
Выберем число
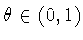 , удовлетворяющее условию
, удовлетворяющее условию
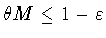 . Построим
. Построим 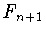 следующим образом.
Возьмем такое число
следующим образом.
Возьмем такое число
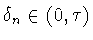 , чтобы выполнялось
неравенство
, чтобы выполнялось
неравенство
Теперь выберем  такое, чтобы
такое, чтобы
Положим
 Для
Для
![$t \in [0, \delta _n]$](img400.gif) имеем
имеем
Обозначим через
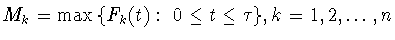 ,
очевидно, что
,
очевидно, что 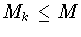 . При
. При
![$t \in [\delta _n, \tau]$](img404.gif) получаем
получаем
Поскольку выражение
при
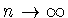 стремится к
стремится к
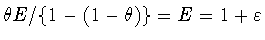 и любая сумма вида
и любая сумма вида
равна
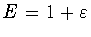 , то это влечет неравенство
, то это влечет неравенство
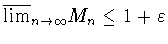 ,
что эквивалентно утверждению леммы.
,
что эквивалентно утверждению леммы.
В следующем пункте нам также понадобится очевидное утверждение.
Предложение 4.1. Если
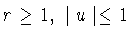 , то
, то
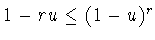 . Если
. Если
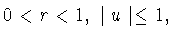 то
то
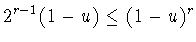 .
.



Next: 5. Доказательство теоремы 2.1.
Up: ТОЧНОЕ НЕРАВЕНСТВО ДЖЕКСОНА-СТЕЧКИНА В
Previous: 3. Некоторые свойства ультрасферического
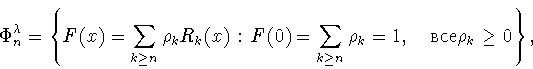
![]() назовем точкой Черныха для
множества
назовем точкой Черныха для
множества
![]() если одновременно выполняются следующие два
условия
если одновременно выполняются следующие два
условия
![]() , в силу равенства
(4.2) Н.И. Черных,
, в силу равенства
(4.2) Н.И. Черных,
![]() . При
. При
![]() и при
и при
![]() оценка сверху в
(4.4) совпадает с неравенством (4.3) В.Ю. Попова,
а при
оценка сверху в
(4.4) совпадает с неравенством (4.3) В.Ю. Попова,
а при
![]() уточняет его, т.к.
уточняет его, т.к.
![]() (см. [40, с.147, (6.6.4)]).
(см. [40, с.147, (6.6.4)]).
![]() вытекает из того, что функция
вытекает из того, что функция ![]() принадлежит
множеству
принадлежит
множеству
![]() и удовлетворяет неравенству
и удовлетворяет неравенству
![]() при всех
при всех
![]() и
и
![]() . Доказательство оценки сверху
. Доказательство оценки сверху 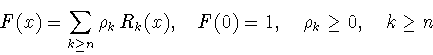

![]() близка к той, которая применялась
В.А. Юдиным в работе [24]. Предварительно мы
определим четную
близка к той, которая применялась
В.А. Юдиным в работе [24]. Предварительно мы
определим четную ![]() -периодическую непрерывную функцию
-периодическую непрерывную функцию
![]() , которую достаточно задать на отрезке
, которую достаточно задать на отрезке ![]()
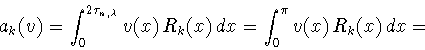

![]() . Положим
. Положим
![]() . Пусть построена функция
. Пусть построена функция
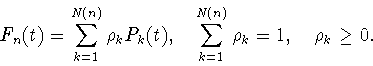
![]() , то
, то
![]() . Если
. Если
![]() то
то
![]() .
.