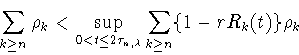5. Доказательство теоремы 2.1.

Начнем с доказательства утверждения (A) теоремы 2.1. Пусть $r\geq 1$, в силу соотношений (1.19), (1.22), (1.15), (1.14) и предложения 4.1 достаточно установить неравенство

$$\sum_{k\geq n}\rho_k < \sup_{0<t\le 2\tau_{n,\lambda }} \sum_{k\geq n}\{ 1-r R_k(t) \} \rho_k$$ (5.1)

для любой последовательности неотрицательных чисел $\rho_k \geq 0, k=n,n+1, \ldots$, удовлетворяющей условию $\sum_{k\geq n} \rho_k =1$. Заметим, что ряд, стоящий в правой части (5.1) можно представить в виде

$$\sum_{k\geq n}\{ 1-rR_k(t) \} \rho_k = \sum_{k\geq n}\rho _k - rF(t),$$

где функция $F(t)= \sum_{k\geq n} \rho_k R_k(t)$ принадлежит множеству $\Phi _n^{\lambda }$ (см. (4.1)). В силу леммы 4.1 точка Черныха для множества $\Phi _n^{\lambda }$ удовлетворяет неравенству

$$\sigma (\Phi _n^{\lambda }) \leq 2 \tau_{n,\lambda }.$$

Следовательно, (см. определение 4.1, часть (a)) для $F$ найдется точка $x^{\ast} \in (0, 2\tau_{n,\lambda })$, в которой $F(x^{\ast} ) <0$. Поэтому справедливо неравенство

$$\sup _{0<t\leq 2 \tau_{n,\lambda } } \left\{ \sum_{k\geq n}\rho_k - rF(t) \right \} > \sum_{k\geq n}\rho_k,$$

которое совпадает с (5.1). Случай $0<r<1$ получается аналогично.

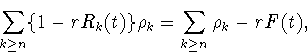
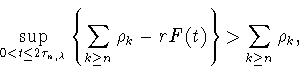
Для доказательства утверждения (B) теоремы 2.1 воспользуемся леммой 4.2 В.В. Арестова. Пусть $r>0,\ 0<\tau < \pi$. Система функций

$$P_k(t)=\{ 1-R_{n+k} (t) \} ^r,\ \ \ k=0,1,\ldots ,$$

как известно (см. [40, с.175, (b). Формула Дарбу, формула(7.32.2)]), удовлетворяет всем условиям леммы 4.2. Поэтому для любого $\mbox{$\varepsilon$}\in (0,1)$ найдется последовательность неотрицательных чисел $\rho_0, \rho_1, \ldots$ такая, что $\sum_{k\geq 0} \rho_k=1$ и

$$\sum_{k\geq 0}\rho_k\left/ \sup_{0<t\leq \tau}\right. \sum_{k... ...1-R_{n+k} (t) \}^r \rho_k \geq\frac{1}{1+\mbox{$\varepsilon$}}.$$

Устремляя $\mbox{$\varepsilon$}$ к нулю, получим требуемое утверждение.

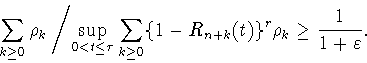
Для доказательства утверждения (C) теоремы 2.1 при $r=1$ достаточно, в силу леммы 4.2, построить последовательность функций $F_N,\ N=n+1,n+2,\ldots,$ вида $F_N(x)=\sum_{k=n+1}^N\rho_k R_k(x),\ F_N(0)=1$ с неотрицательными коэффициентами $\rho_k,\ k\ge n+1$ такую, чтобы при любом $\xi\in(0,\pi]$ выполнялось бы соотношение

$$\Vert F_N\Vert _{C[\xi,\pi]}\rightarrow 0\quad {\mbox при}\quad N\to\infty.$$ (5.2)

В случае $0<r<1$ достаточно будет затем применить неравенство Йенсена $\sum_{k=n+1}^N \rho_k\{1-R_k(x)\}^r\le \left\{\sum_{k=n+1}^N \rho_k\{1-R_k(x)\}\right\}^r,$ $\sum_{k=n+1}^N \rho_k=1, \ \rho_k\ge 0, \ k\ge n+1.$

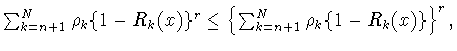
Пример такой последовательности функций можно построить с помощью формулы Кристоффеля-Дарбу (см. [40, гл.3, § 3.2], [41, формулы (1.4), (2.4), (2.5), (2.7), (4.7), (4.14)]), а также равенства (см. [40, (4.7.14)]) $\frac{d}{dt}C_k^\lambda (t)=2\lambda C_{k-1}^{\lambda +1}(t)$ для производных алгебраических многочленов Гегенбауэра. А именно, при $t=\cos x$ положим (см. (3.4))

$$P_k(t)=R_k({\rm arccos }t)=\frac{C_k^\lambda (t)}{C_k^\lambda (1)},\quad k=0,1,\ldots,$$

$$Q_N(t)=\sum_{k=0}^N r_k P_k(t), \quad r_k=\frac{k+\lambda }{\lambda } {{k+2\lambda -1}\choose k}.$$

Следующая последовательность функций $F_N(x)=F_N^*(t),\ t=\cos x,$

$$F_N^*(t)=\frac{Q_N(t)-Q_n(t)}{Q_N(1)-Q_n(1)}= \frac{\sum_{k=n+1}^N r_k P_k(t)}{\sum_{k=n+1}^N r_k},$$

$N=n+1,n+2,\ldots,$ является искомой, т.к. $F_N^*(t)$ преобразуется к виду

$$F_N^*(t)=\frac{2\lambda +1}{2\lambda (1-t)}\cdot \frac{{{N+2\... ...e N}(2\lambda +1+2N)-{{n+2\lambda } \choose n}(2\lambda +1+2n)}$$

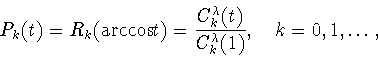
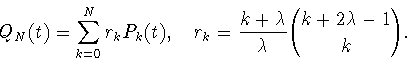
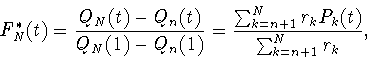
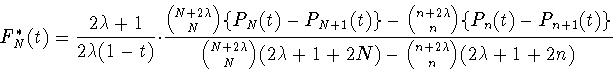
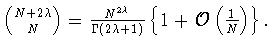и (см., например, [32, с.248]) ${{N+2\lambda } \choose N}=\frac{N^{2\lambda }}{\Gamma(2\lambda +1)} \left\{1+{\cal O}\left(\frac{1}{N}\right)\right\}.$ Теорема 2.1 доказана.

ЗАМЕЧАНИЕ 5.1. Используя (4.6), (4.8), можно получить доказательство утверждения (A) теоремы 2.1 в случае $r>1$ способом, предложенным в работе В.В. Шалаева [39, теорема 1, следствие 1]

ЗАМЕЧАНИЕ ПРИ КОРРЕКТУРЕ. В 1995 г. В.В.Арестов и В.Ю.Попов опубликовали [42] доказательство точного неравенства Джексона-Стечкина в пространстве $L^2({\bf S}^{m-1}),$ $m=3,4,$ аннонсированного ими в [27].

Данная работа обсуждалась в Уральском государственном университете на семинаре под рукодством профессора В.В.Арестова. Автор благодарен профессору В.В.Арестову, а также доценту В.Ю.Попову за полезные обсуждения.