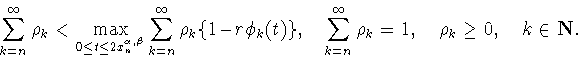 |
(8.1) |
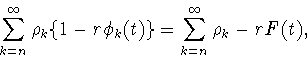
Утверждение (2.2) доказывается аналогично с помощью неравенства
![]() при
при
![]() Теорема 2.1 доказана.
Теорема 2.1 доказана.
Как уже отмечалось выше, неравенство Джексона-Стечкина в
пространстве
![]() при
при
![]() тесно связано с аналогичным неравенством в
пространстве
тесно связано с аналогичным неравенством в
пространстве
![]() комплексных функций, заданных на
единичной сфере
комплексных функций, заданных на
единичной сфере ![]() вещественного евклидова
пространства
вещественного евклидова
пространства ![]() В случае, когда
В случае, когда
![]() различные, указанное неравенство связано с аналогичным неравенством
в пространстве
различные, указанное неравенство связано с аналогичным неравенством
в пространстве ![]() комплексных функций, заданных на проективных
пространствах
комплексных функций, заданных на проективных
пространствах
![]() (при
(при
![]() ) и
) и
![]() (при
(при
![]() ) над полями
) над полями ![]() и
и ![]() вещественных и
комплексных чисел, соответственно.
вещественных и
комплексных чисел, соответственно.