Начнем со сферы. Здесь будет дополнен результат В.В.Арестова
[1, утверждение (B) теоремы 2.2] об оценке снизу константы
Джексона-Стечкина на сфере
![]() При этом мы
будем использовать, в основном, обозначения и известные факты из
гармонического анализа, применявшиеся в [1].
При этом мы
будем использовать, в основном, обозначения и известные факты из
гармонического анализа, применявшиеся в [1].
Итак, пусть
![]() есть пространство комплексных
функций, заданных на единичной сфере
есть пространство комплексных
функций, заданных на единичной сфере ![]() пространства
пространства ![]() со скалярным произведением
со скалярным произведением
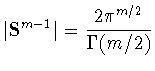 - площадь
сферы
- площадь
сферы
Сдвигом с шагом ![]() называется (см., например,
[44, формулы (1.1), (1.19)]) оператор
называется (см., например,
[44, формулы (1.1), (1.19)]) оператор
![]() , действующий из
, действующий из
![]() в
в
![]() по
правилу
по
правилу
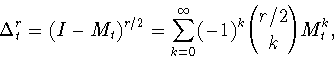
Обозначим через
![]() точную константу
точную константу ![]() в неравенстве
Джексона-Стечкина в пространстве
в неравенстве
Джексона-Стечкина в пространстве
![]()
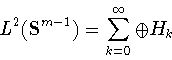
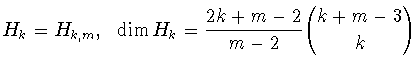 сферических гармоник степени
сферических гармоник степени 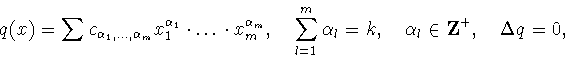
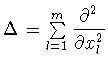 есть оператор Лапласа. Оператор ортогонального
проектирования
есть оператор Лапласа. Оператор ортогонального
проектирования

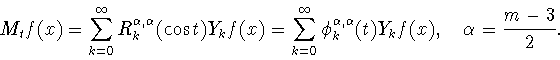
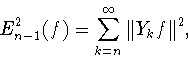
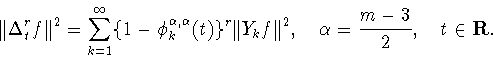
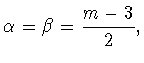 то есть, с учетом равенства (3.4),
имеем
то есть, с учетом равенства (3.4),
имеем
Теперь с помощью первого утверждения следствия 4.1 мы можем
сформулировать отмеченное выше дополнение к результату В.В.Арестова
об оценке снизу константы Джексона-Стечкина на сфере. А именно, в
пункте ![]() теоремы 2.2 из работы [1] условие
теоремы 2.2 из работы [1] условие
![]() можно ослабить, заменив его на условие
можно ослабить, заменив его на условие ![]() Тем самым упрощается формулировка упомянутой теоремы.
Тем самым упрощается формулировка упомянутой теоремы.
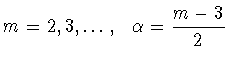 для
каждой функции
для
каждой функции

Замечание 9.1. В силу равенств (9.6) и определения (1.13) все пункты замечания 1.1 естественным образом переносятся и на теорему 9.1.
Перейдем к задаче о точном неравенстве Джексона-Стечкина в
пространстве
![]() комплексных функций, заданных на
вещественном проективном пространстве
комплексных функций, заданных на
вещественном проективном пространстве
![]() Как хорошо известно (см.
[29], [4]), пространство
Как хорошо известно (см.
[29], [4]), пространство
![]() можно отождествить с подпространством всех четных функций
можно отождествить с подпространством всех четных функций ![]() из
пространства
из
пространства
![]() То есть можно считать, что
То есть можно считать, что
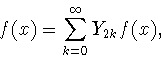
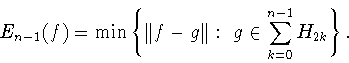
 в неравенстве
в неравенстве 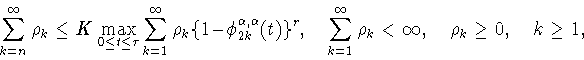
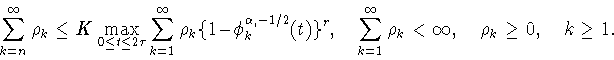
Рассмотрим случай проективного пространства
![]() над полем
над полем ![]() комплексных
чисел. Пусть
комплексных
чисел. Пусть
![]() есть единичная сфера пространства
есть единичная сфера пространства ![]() , здесь
, здесь
![]() - скалярное произведение векторов
- скалярное произведение векторов
![]() из
из ![]() Так же,
как и выше, используя известную (см. [43],
[29], [4]) интерпретацию
Так же,
как и выше, используя известную (см. [43],
[29], [4]) интерпретацию
![]() , в терминах классов эквивалентностей на единичной сфере
, в терминах классов эквивалентностей на единичной сфере
![]() , пространство
, пространство
![]() можно отождествить с подпространством функций
можно отождествить с подпространством функций
![]() которые являются "четными" в следующем смысле
которые являются "четными" в следующем смысле
![]() при
при
![]() и
и
![]() То есть можно считать, что
То есть можно считать, что
Пространство
![]() разлагается в
ортоганальную прямую сумму (см. [4])
разлагается в
ортоганальную прямую сумму (см. [4])
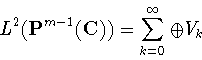
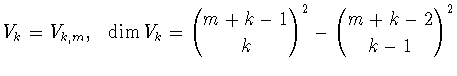 многочленов
многочленов
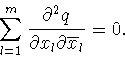
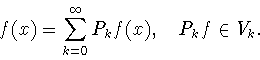
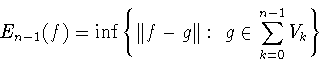
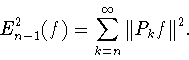
В работе В.И.Иванова и О.И.Смирнова [47, с.101] (см.
также [48, с.100]) доказано, что оператор среднего значения
(см. [49, гл.1, § 4]) (аналог оператора ![]() см.
(9.3)) для функций, заданных на компактных сильно однородных
(или, что тоже самое, духточечно-однородных или дважды однородных)
метрических пространствах, выражается через зональные сферические
функции. В частности, учитывая явное выражение зональных
сферических функций на
см.
(9.3)) для функций, заданных на компактных сильно однородных
(или, что тоже самое, духточечно-однородных или дважды однородных)
метрических пространствах, выражается через зональные сферические
функции. В частности, учитывая явное выражение зональных
сферических функций на
![]() (см.
[37], [29], [4]) через многочлены
Якоби
(см.
[37], [29], [4]) через многочлены
Якоби ![]() получаем, что указанный оператор среднего
значения в пространстве
получаем, что указанный оператор среднего
значения в пространстве
![]() эквивалентен
следующему оператору обобщенного сдвига
эквивалентен
следующему оператору обобщенного сдвига
![\begin{displaymath}{\cal U}_t
f(x)=\sum_{k=0}^\infty R_k^{m-2,0}(\cos 2t) P_k f(x)\,, \quad t\in
[0,\frac{\pi}{2}]. \end{displaymath}](img439.gif)
Далее, по аналогии с тем, как это уже делалось раньше,
на основе обобщенного сдвига
определяются разностный оператор порядка ![]() с шагом
с шагом
![]() и соответствующий модуль непрерывности функции
и соответствующий модуль непрерывности функции
![]() который мы будем обозначать также через
который мы будем обозначать также через
![]() Затем, с помощью теоремы 2.1, получаем
Затем, с помощью теоремы 2.1, получаем
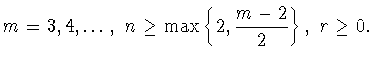 Тогда для любой
функции
Тогда для любой
функции
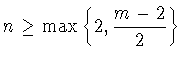 и
и
Из утверждений, содержащихся в работах [47],
[48], [37] следует, что наряду с указанными выше
тремя важными приложениями частных случаев теоремы 2.1,
относящихся к неравенствам Джексона-Стечкина в пространствах
![]()
![]()
![]() имеются, по крайней мере, еще два. А именно, к
задачам о константах Джексона-Стечкина в пространствах
имеются, по крайней мере, еще два. А именно, к
задачам о константах Джексона-Стечкина в пространствах
![]() и
и ![]() сводятся
соответственно аналогичные задачи в пространствах
сводятся
соответственно аналогичные задачи в пространствах
![]() и
и
![]() .
Здесь
.
Здесь
![]() есть проективное пространство над
телом кватернионов
есть проективное пространство над
телом кватернионов
![]() - проективная плоскость
Кэли. Верхние индексы
- проективная плоскость
Кэли. Верхние индексы ![]() и
и ![]() обозначают вещественную
размерность соответствующих многообразий.
обозначают вещественную
размерность соответствующих многообразий.